3 市场结构的计量

    在检验经济学假说、制定或实施公共政策方面。市场结构起着重要的作用。有时候我们想要了解某个市场结构，因为这方面的信息有助于确定在不同情况下使用何种模型才适合于具体的厂商对象。我们常常想要估算某个市场结构，以便能够作出预测，例如，当一项新法律规定某个行业增加一个单位的税后，将会产生怎样的结果。或者，为了了解是否应该实施反托拉斯法来改变目前的行业状况，我们也许想要分析该行业现有的竞争程度。实际上，在涉及到估算行业竞争和垄断程度的各种情况中，我们必须能够描述和计量竞争的程度。为了做到这一点，我们就必须确定衡量竞争和垄断的标准。

    这里有二类问题：

    1．如何描述竞争或垄断？

    2．如何确定能与定义一致的行业？

垄断的涵义

    描述垄断的方法之一是确定与此相对的竞争的各种特征，例如，一个竞争性行业具有如下特征：

    1．没有一家厂商具备控制市场供给的条件，更确切地说，每家厂商都是价格的接受者。

    2  在长期内，不存在经济利润。生产达到长期均衡状态时，边际成本等于价格，并等于平均成本的最低点。

    3．生产同质产品的厂商数目很多，没有进入壁垒。

    当然，我们还可以用另外一些方法来描述一个竞争行业，但是，上述各点至少为我们提供了从垄断者的角度来计量垄断的3条可能的途径：

    1．从事独立活动的能力

    2．绩效

    3．结构

    分析问题的三条途径

    衡量独立活动  首先，我们采用检验厂商控制价格能力（成为价格的寻求者）的方法来定义一个完全竞争的行业。要精确地衡量一个厂商的市场势力通常是困难的，因为它一般要求确立该厂商的需求曲线。

    市场绩效  我们对完全竞争行业所下的第二种定义包括按最低平均成本进行生产，这时价格等于边际成本。我们必须比较价格和边际成本，以确立长期平均成本函数。即使能轻而易举地做到这一点，我们仍然面临着一个颇有意义的工作，即解释每一种特定的市场势力量度实际上说明了什么。

    市场结构  我们可以计算厂商的数目，考察进入壁垒，以便更好地了解某个行业的市场结构。正如我们将会看到的那样，尽管我们可以相对较容易地计算出某个市场中的垄断结构指数，但我们并不总是知道何种量度才是恰当的，我们也并不总是能够解释这种量度。此外，我们还将看到，以各种市场结构指数为基础的预测常常被证明是相当不精确的。

定义产品：是一种可以替代的方法吗？

    衡量市场结构的方法之一是侧重于产品。然而，如果我们选择按照产品来定义一个市场，我们就应当认识到，产品和服务可以是密切相关的，这既来自于消费者方面的消费替代，又来自于市场中生产者方面的生产替代。当产品对消费者和生产者来说都可以替代时，它们就显然可以看作属于同一个市场分类。但情况并非总是如此。让我们举两个在买方和卖方看来替代程度颇为不同的例子。

    1．一个消费者在花费娱乐开支而寻找消费对象时，书籍、音乐会入场券以及一艘钓渔船的租金都被看作是互相替代的。这里很清楚，若从市场的生产者角度看，生产技术的要素替代性却几乎不存在。

    2．再举一个相反的例子，对大多数买者来说，女鞋通常无法作为男鞋的替代品。但是，从生产者方面看，生产要素和技术间却有一些替代性。

    一个折衷 要综合地考虑到生产者和消费者的替代性，一个方法是将市场看成是由消费者的替代物构成的，只有在涉及其他厂商的进入时，才考虑生产者的替代性。这种折衷并不总是产生令人满意的结果，因为有时它允许市场定义中包括替代性较差的产品。这在普查局的药剂分类（S．I．C．2834）中看来尤为突出，正如青霉素不是阿斯匹林的替代品一样，不同种类的维生素片剂之间一般也不能成为替代品。

    弹性计算

    在分析产品之间的替代性时，我们应当进一步提出需求的交叉弹性概念，并把它作为定义经济行业的一种工具。首先我们必须再次定义价格弹性。

    价格弹性的定义  需求的价格弹性是一种量度，用来衡量因价格变化引起的需求量的相对变动。当我们假定需求量和价格方面的变动都极小时，我们就可以定义需求的价格弹性系数（用希腊字母 η或eta来代表弹性）为：

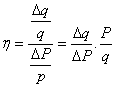
    其中希腊字母  Δ（delta）表示轻微的变动。P是价格，q是数量。

    根据这种定义来计算价格弹性时，弹性的数值与数量和价格的计量单位完全无关。这样我们去比较不同商品的价格弹性就方便多了。考虑一个纯粹天假设的小麦例子。

    设P=5美元／蒲式耳

      q=100蒲式耳

    △P＝1美元／蒲式耳

        △q＝5蒲式耳

    然后方程式（3·1）就变为

    （5蒲式耳/100蒲式耳）

    __________________________________＝0.05/－0.20＝－0.25

    （1美元/蒲式耳）/（－5美元/蒲式耳）

    最后的计算结果没有量纲，它们都被约掉了。

    需求的个别弹性和市场弹性  把单个需求曲线的资料加总，就得出市场需求曲线。正如可以预料的那样，个别需求价格弹性与市场需求价格弹性之间存在着确切的关系。市场的需求价格弹性等于所有个别需求价格弹性的加权平均。权数等于任何既定价格下每一个买者所购买的相对数量，这从下面的例子中可以看出来，设

    X＝x1＋x2                     （3·2）

    其中X是市场的需求量，X1和X2分别是个别需求量。若数量上有一个微小的变化△，则方程式（3·2）变为

    △X＝△x1＋△X2         （3·3）

    方程式（3·3）两边同除以△P，即市场价格有一个微小的变化，再在方程式两边同乘P／X：

      △X/△P·P/X＝（△x₁/△P·P/X）＋（△x₂/△P·P/X）

     （3.4）然后在方程式（3．4）右边的每一项上分别乘以x1／x1和x2/x2：

     △X/△P·P/X＝（△x₁/△P·P/X·x₁/x₁）

     ＋（△x₂/△P·P/X·x₂/x₂）

     ＝（△x₁/△P·P/x₁·x₁/X）

     ＋（△x₂/△P·P/x₂·x₂/X）                           （3.5）

    现在我们把方程式（3．5）整理成一些可以辨认的项：

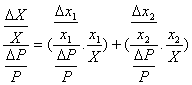                           （3·6）

    在方程式（3·6）中，我们可以看到有3项代表需求的价格弹性，我们还看到x1/X和x2/X这2项只不过分别代表了买者1和买者2在总的市场需求中所占的份额。如果我们用g1和g2分别代表这2个份额，就得到

    η总市场＝g1·η买者1＋g2·η买者2                  （3·7）

    需求的交叉弹性：对替代品和互补品的修正

    现在我们也可以用一种弹性的定义来定义替代性和互补性。迄今为止，我们已经讨论了一种商品的自身价格变动后需求量将如何变化。我们以前所指的是需求的自身价格弹性，现在我们来考察需求的交叉价格弹性，它的定义是

    η_xy＝（△qx/qx）/（△Py/Py）         （3·8）

    下标代表两种商品x和y。当ηxy或ηyx为正，我们就定义这两种商品为替代品，当ηxy或ηyx为负，我们则定义它们为互补品，见图3·1。

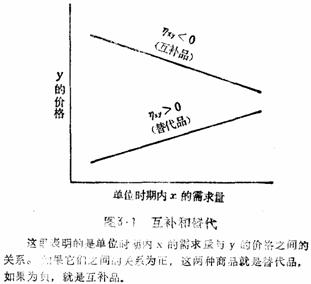
    自身价格弹性的绝对值与交叉弹性之和的关系  我们可以提出一个重要的法则，它说明需求的自身价格弹性的绝对值等于交叉弹性之和，即

      η_XX＝－（η_XY＋η_XZ＋……＋η_XN）               （3·9）

    因此，观察一对需求的交叉弹性并不能使你获得很多有关需求的自身价格弹性的信息。

    在美国控告杜邦公司一案中，里德法官隐隐约约地认识到一种有效的垄断与替代品的交叉弹性总和有关。在这个案例中，政府提供的证据表明，杜邦公司生产了美国玻璃纸销售量的3／4左右，所以认为它构成了谢尔曼法第二款意义上的垄断。   

    但是，当存在着买者为消费目的可以利用的现成的替代市场时，仅仅因为与其他产品不同而被称为垄断的产品，并不构成非法垄断。假如不是这样，那就只有物质同一性的产品才可成为市场的一部分。为接受政府的观点，我们就不得不得出结论，正如防潮玻璃纸制造商一样，平纹布的制造商也是垄断者，诸如此类的还有玻利欧薄膜、铝箔、聚乙烯以及莎纶等，因为这些包装材料中的每一种都是互相有别的。在该案中它们都是证据。当出现与玻璃纸基本上类似的新包装材料时，是否每一种材料都形成垄断？这就要求评价交易中需求的“交叉弹性”……在考虑什么是相关的市场以决定对价格和竞争的控制时，最明确的规则可以说成是：消费者为同一需求而合乎情理地互相交换的那些商品构成了“交易或商业的一部分”，对这部分商品的垄断也许是非法的。

    收入效应和替代效应——总的替代品和互补品  我们可以同时测算价格弹性和收入弹性。算完之后，需求的价格弹性的替代效应和收入效应就显示出来了。设货币收入和其他变量不变，我们可以观察y的价格变化对x需求量变化的影响，这种影响又可以分为收入效应和替代效应两种。在表示需求的交叉价格弹性的方程式（3·8）中，分子部分就是这两种效应之和。因此我们看到的实际上是需求的总交叉弹性，而我们上面的定义指的就是总的替代品和互补品。另一方面，如果方程式（3·8）中的分子只包括y的价格变化对x需求量变化的替代影响，那末我们所考虑的就是需求的净交叉弹性，这时我们的定义指的是净替代品和净互补品。看起来这似乎是一种无关紧要的区分，但在实际计量中，当我们从需求的总交叉弹性转到净交叉弹性时，我们就会发现两种商品可以同时是总互补品与净替代品。如果因为替代影响，y的价格上升引起x的需求量增加，而收入影响所造成的x的需求量的减少，又足以抵消替代影响并有余的话，就会出现这种现象。

    物品x和y也可以同时既是总替代品，又是净互补品。当y的价格上升减少了x的需求量时，就会出现这种局面。然而，如果x是一种劣质品，那么它的收入效应就会增加x的需求量并足以抵消掉替代效应而有余。在实际分析中，一个人选择总的还是净的交叉弹性可能会大大改变他对某个市场中产品所下的定义。

    供给的交叉价格弹性  我们早已提到，投入和技术方面的替代性在定义市场时也许是一个重要的因素。我们可能应该把相关的厂商组合在一起，这取决于一个生产者是否能在其他厂商要价变化后轻易地将资源转向后者生产的产品上。为了能在经验上计量这种组合，我们就必须考察供给的交叉价格弹性，它的定义为

    X生产者提供的x数量变动百分比 / y的价格变动百分比      （3·10）

    该方程看上去与方程（3·8）非常相似，但它们并不是一回事。方程式（3·8）指的是潜在买者的反应，而方程式（3·10）指的是y的价格变动后卖者的潜在反应。这两种计算都不必反映买卖x的实际数量，因为它依赖于x的价格高低，而x的价格在方程式（3.8）和（3·10）中计算交叉弹性时假定是不变的。

    在何处划分界限  让我们假定，在计算中，设其他变量不变以及得到确切的价格和数量变化方面的所有问题都解决了。现在，我们列出一组经过非常仔细地计算的数字，更确切地说，是产品x与所有其他产品的需求交叉弹性。我们对所有正的交叉弹性进行排列，数值最大的在最前面。显然，需求的交叉弹性越大，y和其他产品的替代关系就越紧密。这里仍然存在着一个问题：我们在何处划分界线呢？临界点出现在什么地方，以便我们可以说在该点之后的产品不再属于同一个市场？对此，经济理论无法提供明确的答案。由于在紧密的与松散的替代品之间没有一条明确的分界线，所以任何临界点的确定就成了主观见解、个人判断、甚至是规范经济学的问题了。即使看起来在两者之间、比如第六和第七种物品之间存在着巨大的差异，但是，正如可以在第四和第五种物品之间作出区分一样，这种划分也可以是任意的。

    一个经验性问题  要确定哪些产品是密切的替代品带来了一个经验性问题。我们可以有理由进行推测，但是许多可能的替代品还是定不下来。啤酒真的是萄葡酒的替代品吗？这看起来可能有些道理，但是在确信之前，我们就无须知道需求的交叉价格弹性了吗？

    我们是否应该放弃把交叉价格弹性作为一种标准？上面已经表明，在决定哪些产品应归入同一个市场分类时，任何临界点的确定都是任意的。这种情况是否必然就意味着我们应该放弃计算需求的交叉价格弹性？答案可能是否定的，因为理论和经验上测算的需求的交叉价格弹性可能都符合实际厂商决策。所有厂商都受其他厂商活动的影响，但是只有那些明显影响到某个特定厂商的活动才会得到考虑。如果我们对一群厂商的行为感兴趣，我们可望对厂商进行分组，其依据是，当受到其他厂商影响时，这些厂商各自是如何决策的。在采用需求的交叉价格弹性方法之后，我们就可以发现厂商受其他厂商定价行为影响的程度。采用这种方法，我们还可以推测当厂商在决定各自的策略时，哪些厂商有可能是互相考虑对方行为的。（然而要注意，当其他厂商改变价格、产品质量或广告支出时，需求的高交叉价格弹性并没有告诉我们某个厂商将如何反应。）

绩效量度

    除了上述方法之外，我们可能还希望通过侧重于绩效量度来更直接地计算市场结构。在产业组织研究中，垄断势力的大小是一个重要的变量。在这一部分中，我们将考察三种建立在垄断势力上的市场结构指数：勒纳指数（Lerner index），贝恩指数（Bain index）以及帕潘得里欧指数（Papandreou index）。

    勒纳指数

    阿贝·勒纳为我们提供了一种以垄断势力为基础的计算市场结构的方法，该方法避免了必须从销售资料推算垄断势力的问题。勒纳指数为

    勒纳的垄断势力指数＝[P－MC]/P    （3.11）

    其中P是产品的价格，MC是生产该产品的边际成本。勒纳指数在0到1之间变动，数值越大表明垄断势力越大。这个指数本质上是考察垄断者的行为。它计量的是价格偏离边际成本的程度。例如MC＝5美元，垄断价格＝10美元，则勒纳指数就等于

    10美元-5美元/10美元＝0．5

    或等于50％。

    勒纳的垄断势力指数要求人们能够测量边际成本。至少可以说这不是件容易的事。而且，价格必须与某个质量固定的单位联系在一起，因为质量方面的差异意味着实际价格发生了变动。所以研究者想要通过计算勒纳的垄断势力指数来比较某一行业中的厂商时，他或者她就必须确信能够把产品中所有质量方面的因素数量化。

    对勒纳指数的进一步讨论

    勒纳指数想要计量市场中单个厂商的实际垄断势力，而集中率则是有关整个市场中潜在垄断势力状况的一种量度。

    注意，勒纳指数是实际行为的一种重度，因为它并没有计算该厂商潜在的垄断行为。这种方法建立在比较静态价格的理论上，所以它无法告诉我们目前在价格和边际成本之间的差额是否理所当然地由过去的行为引起，或者说它实际上构成了一个社会成本。

    勒纳指数的问题

    正如图3.2所表明的那样，勒纳指数并不是垄断影响大小的可靠指标。设有两个拥有单家厂商的垄断者Ⅰ和Ⅱ。假定厂商Ⅱ面临的需求曲线等于厂商Ⅰ所面临需求曲线的一半。他们在不同的市场上销售，但都是垄断者。第一个垄断者的需求曲线是DIDI，第二个垄断者的需求曲线是DIIDII，于是该曲线也就成为第一个垄断者的边际收益线，因为它等于DIDI的一半。第二个垄断者的边际收益线是MR。在任何既定的价格水平上，这两家垄断者所面临的需求曲线具有同样的价格弹性。想一下为什么？

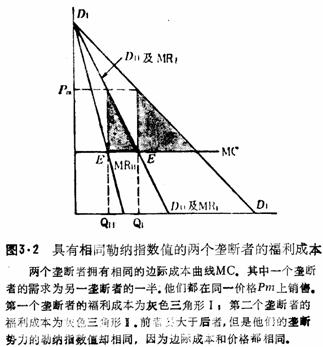
    每一家厂商都会在MR等于MC水平上生产。我们假定有一个共同而且固定的MC，第一家厂商会在MRI与MC的交点，或者在E点生产QI的数量，第二家厂商则在边际收益线MRI1 与MC的交点E’生产QII。于是两家厂商的要价都是Pm。这时勒纳的垄断势力指数就会相等，因为（PI－MCI）/PI＝（PII－MCII）／PII。然而，它们各自的福利成本，正如左边三角形Ⅰ和Ⅱ所显示的那样，是大不一样的。垄断者Ⅰ的福利损失或成本（有时说成是额外的净损失），要比垄断者Ⅱ大得多。

    贝恩指数

    现代产业组织理论的先驱之一乔·S·贝恩曾提出通过考察利润来确立垄断势力的大小。他的理由是，在一个市场中，若持续存在超额利润，一般就反映了垄断的因素。与测量需求的价格弹性或边际成本相比，现成的利润统计资料是容易找到的。当然，一个问题是，经济学家所说的经济纯利润，与会计角度上的利润不是一回事。因此，为了能够计算超额利润，人们至少必须把会计上的利润换算成资本的机会成本或正常的收益率。贝恩把会计利润定义为

    π_A＝R－C－D     （3.12）

    其中

    R＝总收益   

    C＝当期成本   

    D＝折旧

    于是超额利润或经济纯利润的定义就等于   

    π_e＝R－C－D－iv   （3.13）

    这里 v＝业主的投资额

    i＝从投资中可以获得的收益率

    因此利润率就等于π_e /v

    贝恩指数与勒纳指数之间的关系

    上述利润率看来是和价格与平均成本之间的差额有关的。让我们回顾一下，勒纳指数考察的是价格与边际成本之间的差额，所以这两种指数似乎是一回事（如果MC＝AC）；但是这两者之间存在着一个基本区别。一个纯粹或非纯粹的垄断者可能持续获得经济利润，但是并不是说必然会得到这种利润。而且，如果对他或她的产品需求不足的话，即使是一个纯粹的垄断者也无法获得经济利润。所以贝恩指数是不确定的，这是因为虽然持续的高额经济利润率可能表示有垄断存在，但缺少这种经济利润并不就意味着垄断势力消失了，它告诉我们的是可能的垄断势力而不是对垄断势力的直接计量。

    帕潘得里欧指数

    安德烈亚斯·G·帕潘得里欧曾经提出用一对度量指标来刻画垄断势力。这种计量万法建立在需求的交叉价格弹性基础之上。

    然而，帕潘得里欧并没有用方程式（3·8）那样的方法来计算需求的交叉价格弹性。他指出，用那种方法来计算纯粹垄断者与完全竞争的厂商，其结果是一样的。因为在纯粹竞争情况下，第i家厂商并不能影响第j家厂商的销售，原因在于第i家厂商实在是太小了，它的价格无法对其他厂商产生影响。于是两家竞争性厂商之间的需求的交叉价格弹性就等于零。但是按照定义，由于纯粹垄断者没有出售相似替代品的竞争对手，他或她的产品与其他厂商产品之间的需求的交叉价格弹性也是零。因此，对市场结构中的两个极端情况来说，计算出来的需求的交叉价格弹性结果是相同的。

    而且，帕潘得里欧还指出，这种简单化的需求的交叉价格弹性计量法不能说明某个厂商受到自身生产容量约束的情况。换句话说，在某个厂商能从一家或数家其他厂商那里抢走多少生意方面存在着某种界限，这只不过因为存在着短期内生产扩张的限制。简单化的需求的交叉价格弹性所计量的是通过降低价格来掠夺其他厂商份额的潜在能力，但它并没有告诉我们潜在的供给如何，因为要计量供给就需要知道生产能力。

    渗透系数  帕潘得里欧提出，通过估算渗透系数，我们就可以描述因其他厂商价格变化引起某家厂商销售量变动的幅度。这个指数计算的是一家厂商渗透进竞争对手的市场的能力。

    稳固系数  同一问题的另一方面是一个厂商抵挡其他厂商类似渗透的能力。在同时考察了这两个系数之后，帕潘得里欧就能够描述不同程度市场势力的各种组合。然而，在实际的行业和厂商研究中，没有几个研究者能找到应用这些指数的方法。

对集中的量度——同一行业中的一组厂商

    按照产品或绩效量度来定义市场时所遇到的种种困难，促使经济学家、政策制定者以及其他人寻找另外的计量方法。随着时间的推移，人们已逐渐趋向于侧重考察一个行业中的厂商规模分布状况，而行业中的厂商规模分布状况又归结到一个简洁的行业集中量度上。

    在产业组织理论中，我们常常可以看到“市场集中”、“经营集中”以及“经济集中”等术语。在描述我们经济中某个或数个部门的竞争程度时，“集中”这一术语或概念看来是最重要的工具之一。衡量行业集中的方法很多，最常见的是最大4家或8家厂商在总销售或总就业中的比重。于是一个80％的4家厂商集中率——正如人们这样讲的——就意味着比50％的4家厂商集中率有更大的垄断势力。就其本身的含意来看，较高的集中率表明有更多的销售额或其他经济活动指标控制在很少一部分厂商手中。这种关系反过来又与下列看法联系在一起：在合谋实行增加行业收入的卡特尔策略方面，既存在着冲动也存在着机会。一个拥有25家厂商的行业例子如下：

    销售额

    第1家厂商150000000美元

    果2家厂商100000000美元

    第3家厂商80000000美元

    第4家厂商70000000美元  1-4家共计400000000

    第5家至第25家厂商150000000美元

    总计550000000美元

     4家厂商集中率＝400000000/550000000＝81．8％

    尽管初看起来集中率似乎是一个有用的垄断势力量度，但它有一个严重问题。垄断势力不仅是单个厂商市场份额的函数，它也是来自现有厂商和可能进入该行业厂商的潜在供给的函数。正如保罗·萨缪尔森指出的那样，一个由单家厂商构成的行业的集中率可以是100％，但是如果潜在的供给弹性足够大的话，该厂商的垄断势力可以为零。换句话说，如果存在着一种能带来垄断利润的价格，那么现有的垄断就会受到新进入者或该行业中原有边际厂商扩张引起的洪水般的冲击。

    较大部门中的集中

    上面我们考察了4家厂商的集中率，但是我们也可以考察最大8家、20家或者50家厂商拥有或控制的份额。在各个制造行业中，我们可以找到1947、1954、1958、1963、1966、1967、1970以及1972年的集中率资料。你也可以查看整个制造业的集中情况。我们可以得到制造业中那些50万家厂商的制造行业中最大20家、50家、100家以及200家所占份额的资料。当然，这种总量计算法也包含了我们早先提到的那些问题。例如，几家最大厂商所占份额的上升意味着什么？制造业中剩余部分变得更大说明了什么？一些大厂商与其他厂商合并又意味着什么？而且，我们将会看到，这样一种量度几乎不能作为预测该行业中采取的策略或绩效的依据。由于最大几家厂商的相对地位在变动，所以不同时间的比较也是一个问题。

                表3．1不同行业中的集中率（％）

                            最大几家厂商所占发货值的比重

                            最大4家厂商      最大8家厂商

                           1967   1972         1967   1972

    汽车                     92     93           98     99

    原铜                     77     72           98     a

    飞机                     69     66           89     86

    合成橡胶                 61     62           82     81

    高炉与轧钢机             48     45           66     65

    工业用卡车及拖拉机       48     50           62     66

    建筑机械                 41     43           53     54

    石油                     33     31           57     56

    造纸                     26     24           43     40

    肉类加工                 26     22           38     37

    报纸                     16     17           25     28

    液体乳制品               22     18           30     26

    各单个行业集中率之间的关系可能也有问题。例如，当我们从4家厂商集中率改为8家厂商集中率后，各行业集中率的相对次序可能会发生变化。在表3．1中，我们通过一个例子来说明建筑机械行业与石油行业之间是如何发生这种次序变动的。尽管如此，各行业中一个简明的最大4家或8家厂商的集中率指数排列通常还是说明了相对集中的大小，它大致上符合用任何其他控制单位的绝对数来计算集中率所得到的排列结果。

    计量规模大小：资产、收入以及劳动力

    我们可以通过计算经营资产、经营收入、雇佣人员的数目来衡量对一个行业或整个经济的控制集中状况，下面我们就提一下这3种对应的集中计量方法。哪种统计资料最容易获得就决定了哪种集中率较为通行。例如，当我们研究对整个经营活动的控制集中时，一般说来我们是从总经营资产的控制，而不是从经营收入或劳动力的控制入手的，这主要是因为经营资产方面的资料较易获得。

    选择不同的变量来计算集中引起了新的行业位次先后问题。人们可能会发现，把资产作为基本计算变量，与用雇佣人员数作为计算变量所得到的位次先后是不一样的。

    阐明市场定义的问题  我们在上面曾经指出，在定义和计量市场时出现了一个令人头痛的问题。当我们考察集中时，这个问题变得格外麻烦。我们所使用的市场定义方法可能会得到，也可能得不到一个精确的（在解释或预期厂商行为方面很有用的）集中率。在大多数情况下，我们会发现，对市场的定义越是狭窄，计算出来的集中率也就越高。大多数公司都从事一定程度的专业化生产。即使它们在追求多样化时也同样如此。例如，如果我们现在观察酒精饮料市场，我们可能就会发现有些厂商专门生产葡萄酒，有些专门生产啤酒，有些则专门从事所谓硬酒的生产。如果我们使用的是一个定义宽泛的市场，如酒精饮料市场，那就很可能得到一个低值集中率。如果我们单独考察葡萄酒、啤酒或硬酒市场，那集中率肯定会上升。如果我们定义的市场甚至更为狭窄，研究白葡萄酒与红葡萄酒，或波旁酒与杜松子酒的市场，那么集中率通常将会更高。

    空间隔离

    一个来自结构性垄断势力的高值集中率可能因空间上的隔离而引起。水泥行业是一个明显的例子。4家领先厂商占有全国水泥销售量的30％。但是若从单个工厂的角度看，有90％的水泥是运往160英里以内区域的。当全国被分成51个地区时，其中只有3个地区得到领先4家厂商的供应，而且，这4家厂商占这些地区的销售额还不到SO％。

    选择确切的市场  由于全国的和地区的集中率有很大区别，所以选择恰当的市场就很重要。从表3．2中可看到，地区性的市场，如东部、中西部以及西北部市场，每个市场的集中率都是85％，但是从全国性的市场来看，最大4家厂商（第1、2、3以及第6家厂商）的销售额加总为205个单位，或者说集中率只有68％。规模相似的地区性市场的数目越多，则从全国性市场以及从每一个次级市场计算的集中率差异就越是显著。例如，若50个州中分别存在着规模大致相同的垄断性市场，每个州的市场集中率指数为100％；然而，把全国作为一个68％整体来考察，那么4家厂商的集中率就只有8％多一点了。

              表3．2地区性市场和全国性市场的集中

                  地区性市场

           _________________________

    厂商    东部    中西部    西北部      全国市场

      1      40      20         5           65

      2      20      20        10           50

      3      15      20        15           60

      4      10       0        35           45

      5      10      15        15           40

      6       6      25        20           50

    最大4家  85      85        85           205

    总计     100     100       100          300

    最大4家集中率85％    85％      85％         68％

    一条走出两难困境的途径  为了避免低估一个范围较广的市场集中情况，我们可以看一下各个次级市场的加权平均集中率。我们用各个次级市场所占份额的加权平均集中率来表示这个范围较广的市场，而不是把每个次级市场简单地加总。尽管如此，这个方法还是会在一个定义宽泛的市场上夸大集中程度。从根本上说，我们现在正试图通过改进计算方法来解决一个理论问题。寻求恰当的市场定义的方法应该靠我们的理论，而不是靠计算上耍的花招。

    为一般人所忽视的供给者  有关集中率的另一个问题是人们通常都忽视了两种极其重要的替代供给来源：来自国外的进口商品以及用过的或废弃的物品。对国外竞争者的忽视所造成的重要影响已由西奇尔（Sichel）和马费尔斯（Marfels）作了经验论证。他们两人的研究都表明，如果外国竞争被忽略不计，就会产生过度夸大集中率的现象。

    同样地，对来自废旧物品卖者的竞争的忽视也会夸大集中。可是这类分析很复杂，因为新产品的供应者在生产中并非不考虑废旧物品作为供给的一个竞争来源所造成的后果。消费者在购买新产品时，也并非没有忽视旧货的价值。

其他各种集中指数

    我们早已讨论过应用得最为广泛的经营集中指数，它与一个行业中最大4家或最大8家厂商所占资产或销售额的百分比直接联系在一起。除此之外，还存在着一批被称为汇总计量法的集中指数，它们用来检查在任何集中率既定的市场中，厂商规模的分布是否均匀。这些指数涉及到一个行业中所有厂商的分布，并与各种离散统计概念有关。不少研究者已经搞得很深，他们认为集中与厂商规模不均匀的离散是同义语。当然，并非所有的研究者都同意这说法。尤其是，阿德尔曼（Adelman）强调指出，离散没有实在的经济后果。确切地说，他认为离散所计算的只不过是行业中实际厂商数目，传统的垄断和寡头模型强调的是厂商数目稀少，因此是支持阿德尔曼的观点的。

    尽管这样，各种研究都在有意表明一个行业中厂商规模的不对称现象基本决定了市场中所有厂商的行为和举动。

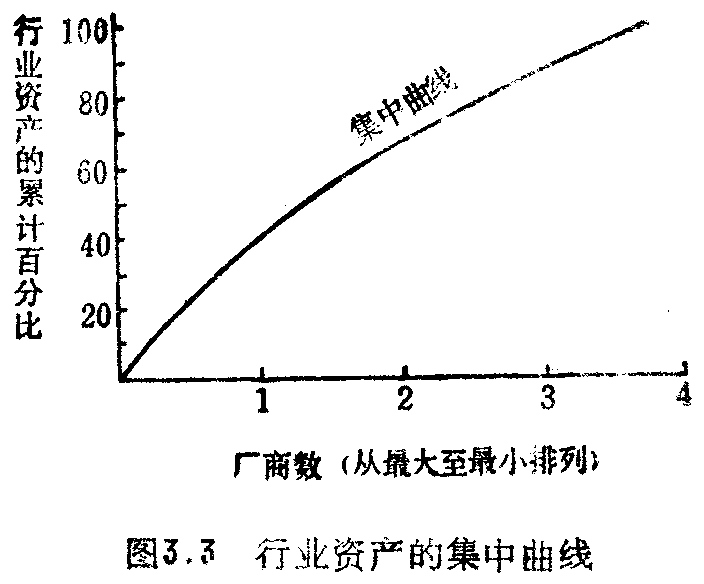
    集中曲线

    如果我们累计一个行业中领先厂商占整个行业资产的百分比，我们就得到了一条曲线，它被定义为集中曲线。让我们看图3．3，这是一条虚设的XYZ行业的集中曲线。该行业由4家厂商组成，其资产分别是4000万美元，2500万美元、2000万美元和1500万美元。横轴表示厂商的累积数目，按最大到最小向右排列；纵轴计算这些厂商占行业资产的百分比。我们也可以方使地按雇佣人员数或总销售额来描绘集中曲线。

    相对于一条上升缓慢的曲线来说，一条陡峭上升的集中曲线代表了较高的集中程度或绝对集中。当在同一张图上比较两个行业时，若其中一条集中曲线总是在另一条之上，则该曲线代表的行业的绝对集中水平就较高（然而，当两条曲线相交时，关系就模棱两可了）。显然，为了能够比较两个不同行业或者是同一行业中不同时点的集中率。我们必须采用总资产的百分比而不是具体的美元值。采用总资产百分比的缺陷在于当我们比较两个行业时，我们看不出正在比较的行业中哪一个在经济上更为重要。在同一张图上描绘比较炼钢业与马蹄铁行业的集中曲线难道是有意义的吗？

    洛伦茨曲线

   大多数初学经济学的学生在学习收入和财富的分配时就接触到了洛伦茨曲线（Lorenz Curve）。洛伦茨曲线讲的是市场总发货值的百分比与市场中由小到大厂商的累积百分比之间的关系。

    现在我们把洛伦茨曲线的思路应用于一个假想的市场中，见图3．4。在纵轴上，我们标的是自最小厂商开始的厂商累积百分比。把它与图3.3——表示集中曲线——中的横轴作个比较，那里我们考察的是从最大厂商开始的厂商累积数。图3．4中的纵轴则与图3．3中的纵轴完全一样。

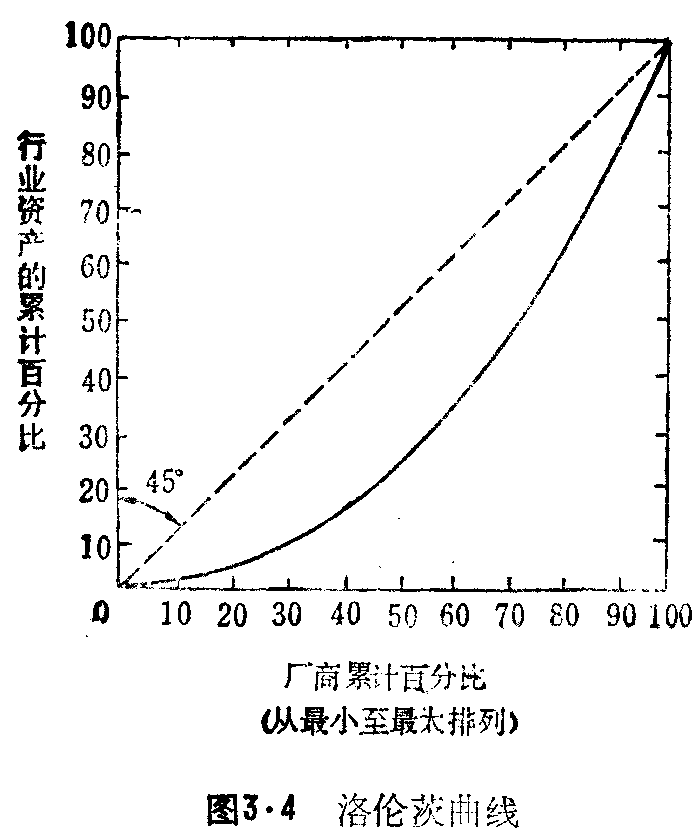
    图3．4中的对角线代表一个厂商资产规模均匀分布的行业。换句话说，如果洛伦茨曲线与对角线重合，则所有厂商都具有相同的规模。当曲线凸向右下角时。就分别表示任何特定的厂商规模分布不均匀的市场。然而，可以想象，在一个仅由少数几家规模相同的厂商构成的行业中，也可以出现高度集中的情况。这就是为什么表示行业中厂商累积百分比的洛伦茨曲线常常被称作是一种不均匀的、或者说是相对集中的量度的原因。也就是说，洛伦茨曲线计量的是相对集中而不是绝对集中，后者由前几节讲到的集中率或集中曲线表示。

    作为一种汇总指标，洛伦茨曲线显然无法表示任何寡头和集中的增长情况。尽管大多数经济学家相信销售者数量的减少增长了集中，但是一个统计学家却可以从洛伦茨曲线上证明销售者数量的减少降低了相对集中。这里相对集中与绝对集中之间的区别就显然可见了。行业中厂商数目的减少使得剩余厂商在规模上更接近了，于是在绝对集中上升时，相对集中或不均匀却下降了。而且，一些经济学家相信，在某些行业中，还存在着一大批与行业巨头相比“无足轻重”的厂商，这些经济学家坚信，任何改变了这些无足轻重厂商数目的集中计量是没有意义的。

    裁减指数  解决这个问题的一个办法是使用裁减指数。例如，人们也许要考察能达到75％行业产出的那些最大厂商的数目。这个方法在指标中裁掉了所谓边际厂商。人们推测，这样一来，行业与行业之间的厂商数目差异将变得极小。

    基尼系数

    基尼系数（Gini Coefficient）是建立在洛伦茨曲线基础上的一个统计量。我们可以用表示洛伦茨曲线的图3．4来说明基尼系数的概念。我们把45度对角线与代表实际厂商资产分布的洛伦茨曲线之间的面积与对角线以下的整块面积——即图3．4中矩形面积一半的三角形——作比较。换句话说

    表示不均等的基尼系数=对角线与代表实际收入分配的洛伦茨曲线间的面积 / 对角线以下的三角形面积

    这个比值意味着什么呢？它意味着基尼系数值可以从0变到1。如果厂商规模的分布完全均等，则基尼系数等于0，因为，对角线或曰绝对均等线与实际厂商资产分布的曲线之间的面积为零。然而中间这块面积越大，基尼系数值也就越大，于是就计量了不均等的程度。作为不均等的一种指数，在势均力敌的厂商数目较少时，从基尼系数中似乎可以推出有道理的结论。一个拥有相同市场份额的双头或三头寡头行业的基尼系数为零，然而这些厂商所在的行业肯定不能被看作竞争行业。而且洛伦茨曲线的形状，以及相应的基尼系数值，很容易因错误定义行业中的厂商数目而受到扭曲。随着研究中包含的边际厂商数目的减少或增加，显示出来的不均等程度倾向于变得更大。还要注意，2家各自生产50％行业产量的厂商会与100家分别生产1％行业产量的厂商具有同样的基尼系数，它们都为零。然而，按照一般的推测，这两种情况下的行业行为是大不一样的。

    基尼系数的应用  基尼系数被应用于大量的实际研究之中，如霍罗威茨（Horowitz）、沃伊廷斯基（Woytinsky）以及肯普（kemp）的研究。

    基尼系数的问题  基尼系数面临的问题与所有汇总集中指标面临的问题相同：需要得到市场中每一家厂商所占份额的确切资料。因为普查局不允许公布任何包含个别公司数据的统计资料，通常我们是得不到具体资料的。此外，从两条不同的洛伦茨曲线可以得出相同的基尼系数，只要它们所围的相对面积大小是相等的。所以，与其他只含一个参数的计算方法一样，在一个既定的市场中，基尼系数并不代表唯一的厂商规模分布。

    赫芬达尔指数

    另一个流行的厂商规模离散量度是赫芬达尔指数（Herfindahl Index）。这是O·C·赫芬达尔1950年在哥伦比亚大学的一篇博士论文中提出来的，那篇论文的题目是“钢铁业中的集中”。赫芬达尔汇总指数定义为一个行业中各厂商所占行业总资产百分比的平方和，即

    赫芬达尔指数＝        （3.14）

    其中N是厂商数目

    x_i是第i家厂商的绝对规模

    T是市场的总规模

    于是我们看到，分数x_i／T只不过是第i家厂商占整个行业资产、销售或其他变量的百分比。

    让我们举一个例子。在一个既定的市场中，总资产等于1000，共有4家厂商，它们的绝对规模分别是500、350、100和50，那么这个市场的赫芬达尔指数就等于0．5²＋0．35²＋0．1²＋0．05²，或者说等于0．385。

    当所有的厂商都具有相同的规模时，该指数就变为1／N如果行业中只有一家厂商。则赫芬达尔指数等于1。

    计量市场份额的变动 斯蒂格勒证明赫芬达尔指数可以用来计量市场份额的变化。这个指数包括了市场中所有的厂商，它与其他计量垄断势力的方法有相似之处。虽然这个指数知名度较高，但是由于资料要求方面的问题，所以难以进行经验分析。当然人们可以用几家最大厂商的有限资料来计算一个最起码的赫芬达尔指数。

    赫芬达尔指数倾向于一种急剧偏向低值的分布。除非垄断势力分布不均等，采用这一指数很容易看出市场份额的变动差异。

    其他指数

    还有一批试图刻画同一行业中厂商规模离散程度的指数。我们简要地来看一下其中的几种。

    相对平均偏差的截取  行业资产（或销售、或雇佣用人数）的分布可以看作是一种统计上的离中趋势，它计算行业中每家厂商的资产（或销售、或雇佣人数）偏离平均规模厂商资产的程度。从统计上看，所有偏离平均数的数值之和总是为零。因此我们应该把这些偏差的绝对值（不管其正负号）加以平均，以便得出一种离中趋势的量度，它常常被叫做平均偏差。接下去，平均偏差除以平均数，就得到了相对平均偏差。

    皮特拉比率（Pietra Ratio）、普霍斯差异（Prais Disparity）以及随机指数  有一种与相对平均时期截取有关的不均等指数，叫做皮特拉比率。另一种指数，即普雷斯差异，讲的是最大厂商与最小厂商之间的差异越大，则集中程度越高。

    尤尔（Yule）、帕雷托（Pareto）以及对数正态指数计算的是一个由随机增长过程决定厂商分布的行业集中。

我们怎样来定义行业？

    现在我们可以来着手处理定义市场以及区分市场与行业这样一个棘手的问题了。

    标准行业分类体系

    许多有关产业组织假说的研究都使用了制造业普查的统计资料。通过行政管理和预算局（OMB）领导的一个工作小组的努力，美国政府提出了一种精致的标准行业分类（S．I．C．）数码体系。在这个体系中，每个数码代表了不同经营活动的产出。厂商一旦被归入S．I．C．数码中，它们的销售、资产或发货值等资料就要集中起来，以便汇总形成行业的统计资料以及行业结构的量度。其他国家和某些国际组织如联合国都有各自的标准行业分类，用以进行正式的统计。例如1968年，英国的标准行业分类就包括了27种主要的行业组，它们再被细分成181个亚组。在美国，S．I．C．体系由一组7位数的数码构成，任何分类的第一个数字代表经济部门，例如5代表商业，0代表农业和林业，2和3代表制造业。就制造业内部的厂商来说，前2位数字一起代表一个制造业中的产品分组，这样的制造业分组有20个，从20至39。2位数的行业分组共有99个。数码的前3位数字则进一步对上述分组进行划分，然后有5位数，直至7位数。7位数代表了7500来种不同的产品。在表3．3中，我们列出了2位数S．I. C．中的制造业分组。在表3.4中则把一个特定的2位数S.I.C.进一步细分成3位数和4位数。表示汽车部件及附件的4位数行业构成（S．I．C．NO．3714）列在表3.5中。 

表3．3 S．I．C．2位数制造业分组

___________________________________________

    制造业

    大组  20  食品及类似产品

    大组  21  烟草制品

    大组  22  纺织品

    大组  23  服装及其他各种纺织制成品

    大组  24  木材及木材制品（家具除外）

    大组  25  家具及室内固定装置

    大组  26  纸张及相关产品

    大组  27  印刷、出版及相关产品

    大组  28  化学品及相关产品

    大组  29  石油提炼及相关产品

    大组  30  橡胶及各种塑料制品

    大组  31  皮革及其制品

    大组  32  石材、陶土、玻璃及水泥制品

    大组  33  金属冶炼业

    大组  34  金属加工制品（机械及运输设备除外）

    大组  35  机械（电气除外）

    大组  36  电气及电子机械设备

    大组  37  运输设备

    大组  38  各种计量、分析和控制仪器；摄影、医疗及光学仪器；钟表

    大组  39  其他各种制造业产品

__________________________________________

表3.4  S．I．C．2位数以及3位数、4位数分组

37  运输设备

371 汽车及汽车设备

    3711汽车及客车车身

    3713卡车及公共汽车车身

    3714汽车部件及附件

3715载重汽车

372飞机及部件

    3721飞机

    3724飞机引擎及其部件

3728飞机部件及辅助设备（其他地方未归类过的）

373 轮船建造及修理

    3731舰船建造及修理

3732气艇建造及修理

374 铁路设备

3743铁路设备

375 摩托车、自行车及其部件

3751摩托车、自行车及其部件

376 导弹、航天飞行器及其部件

    3761导弹及航天飞行器

    3764导弹、航天飞行器的推进器及部件

3769导弹和航天飞行器的部件、辅助设备（其他地方未归类过的）

379 其他各种运输设备

    3792旅行用的挂车及拖车

    3795坦克及其部件

    3799尚未分类的其他运输设备

________________________________________

表3.5 S．I．C．4位数汽车部件及附件

___________________________________________

    3714汽牛部件及附件

    指主要从事于汽车部件及附件制造，但不制造整车或小客车车身的企业。主要从事于汽车、卡车整车制造或组装的企业归入3711行业分类，制造内外胎的企业归入3011行业分类，汽车玻璃归入32大分组，汽车冲压件归入3465行业分类，汽车照明设备归入3647行业分类，点火装置归入3694行业分类，蓄电池归入3691行业分类，汽化器、活塞、环圈以及阀门归入3592行业分类。

汽车上的加速装置              汽车上的备用车轮

汽车上的汽闸                  汽车上的汽油、燃油及空气过滤器

除点火装置外的汽车成行导线装置    汽车车架

汽车上的轴和轴套              汽车燃油泵

汽车车轴                      汽车燃油装置及部件、油箱、

汽车轴承（滚珠和滚轴除外）    油管及歧管

汽车上的制动鼓                汽车油箱

汽车上的大小保险杆            汽车调速器

汽车上的凸轮轴                汽车加热器

汽车上的阻气门杆              汽车车篷

汽车上的空气滤清器            汽车喇叭

汽车引擎的连杆                汽车驾驶用的液压动力泵

汽车上的曲轴组装件            汽车上的仪装板组装件

汽车上的气缸盖                汽车上的润滑器及部件

汽车上的除霜器                汽车上的歧管

汽车上的差动装置及部件        经工厂重新装配的汽车引擎

汽车上的方向信号装置          汽车部件及附件（汽车冲压件除外）

汽车上的驾驶杆                汽车上的排气消声器

汽车上的引擎及部件（内燃机    汽车上的滤油器

除外）                        汽车上的油管

汽车上的排气装置及部件        汽车上的动力传送装置

汽车上的散热器、冷却器罩壳    汽车轮胎阀门芯

及冷却机芯                    汽车顶盖（金属冲压件除外）

汽车上的后轴套                汽车上的传动装置、机壳及部件

经工厂重新装配的汽车引擎和    汽车传动装置

传动装置                      汽车上的万向节

汽车轮辋                      汽车上的真空匣

汽车安全用的撤沙器            车轮

汽车上的减震器                汽车上的挡风玻璃架

汽车上的驾驶装置              各种挡风玻璃上的刮水器

汽车上的备用轴及第二个备用    冬季用散热器前的保温罩

轮                            汽车成行导线装置（点火装置除外）

汽车上的拉杆

————————————————————

    S．I．C．体系的用意在于把有关行业和产品的资料都归在一个有意义的体系中。该体系不随时间而变化，这样现在的资料就能与过去的资料相比较。必须记住，行业和产品分类并不是经济理论或机械呆板的规则的产物。实际上，以前产业界代表与政府官员的商谈常常就在于确定哪些产品和厂商应归入哪一个分类。人们同样还应该记住，制订S．I．C．体系的目的并不是为了研究行业集中，而是为了普查报告及其他政府统计。

    定义一个行业的基本侧重点是在供给方。大多数行业是按照厂商所“从事生产的一种或一组产品”未定义的，它们与生产的技术过程或使用的原材料有关。因此一个市场的定义是从供给方的替代性来加以考察的。在许多情况下（如果不是全部的话，消费者方面的替代性看来是完全被人们忽视了。参议院的一个小组委员会在“关于美国行业集中的报告”中指责用S．I. C. 分类来研究集中率：   

    本报告并不想使普查分类符合于各个行业市场中的实际竞争结构。在某些情况下，这种分类的结果相当准确地反映了市场集中的程度，在另一些情况下，则夸大或低估了这种集中。……就某些分类来说，集中的计量可能非常有意义，它指出了相对的市场势力。对其他一些分类来说，这种计量则没有任何意义。

    用行业法和产品法来分类

    在确定市场分类时，政府使用行业法和产品法。按照前一种方法，根据获自企业的资料情况，每家企业分别归入43个4位数行业分组之中。划归某一行业的依据是企业的主要产品或经营活动的类型。然后该企业所有的产品都被包括在那个行业分类之中。按照产品法，不管企业主要的产品生产活动是什么，特定产品的产量归入一个总的产品分组中。换句话说，即使企业本身应该划归唯一的一个基本行业组，但事实上任何企业的产品都分别划入相应的产品分组中去了。

    在使用产品法及行业法来分类对，方法的不同引起了两种差异。按照行业法，有些归入某个行业分组的产品显然并不属于该行业。另一方面，按照产品法，企业产品总量中包含的产品可能并不是该企业的主要产品。这种情况告诉我们，政府定义的4位数行业分类并不能与它们派生的5位数产品分类进行比较。为了确定这些差异的大小如何，普查局提出了两种被称为覆盖率和专业化率的“差异”量度。

      覆盖率  覆盖率的定义是某个行业的主要产品市场中来自特别划入该行业工厂的比重。其定义如下：

     覆盖率＝划归X行业的工厂生产的X产品的发货额 / X产品的总发货额

    因此，举例来说，1972年商用洗衣设备方面的某种覆盖率，如0．70，说明有70％的商用洗衣设备来自该行业的工厂。

    专业化率 专业化率又叫主要产品的专业化率，讲的是划归某个行业的工厂实际上专门从事生产该行业主要产品的程度。其定义如下： 

    专业化率＝划归X行业的工厂生产的X产品发货额 / 划归X行业的工厂的总发货额

    1972年商用洗衣设备行业的专业化率为0．91，这意味着划归该行业的工厂生产的产品中，实际上有91％是商用洗衣设备，或者说该行业的产品中有9％是由其他产品构成的。这些比率在不同的时期可能会变动。例如1947年商用洗衣设备的覆盖率和专业化率都为0．94。

    专业化率越低，行业中工厂的生产就越是多样化。例如，油漆及类似产品行业的专业化率为60％，这说明该行业工厂的产品中有40％是由非油漆及类似产品构成的。

    资料问题

    经济学家在讨论市场概念时，一个市场的产品范围经常占有支配地位。每一个市场既有时间范围又有空间范围。我们可以把一个市场定义为厂商的组合，对相同的潜在购买者来说，其中每一家厂商借给的产品都具有一定程度的替代性。

    市场不等于行业  “市场”这个术语或某个经济学家定义的行业不一定必然与OMB工作小组或S.I.C定义的行业相同。同一行业中的厂商毕竟是可能生产非替代品的。事实上，他们可能对极不相同的消费者集团销售其产品。此外，我们将会看到，除了人们正在分析或被联邦政府归类的那种产品外，同一个S·I·C·行业中的厂商可能还生产其他产品。例如，按其主要产品类型来说，威斯汀豪斯公司被划归为电气产品及设备的供给者，可它也生产煤气焚化炉以及夹板。但是根据S．I．C．体系的划分方法，所有威斯汀豪斯公司的资产都归入电气产品及设备。由于行业资料常常被用来检验市场行为的含义，因此在进行经验研究时就显然存在着困难。总之，某种产品的经济市场或行业不一定与统计上生产该产品的行业定义一致。

    进出口  所有的经验研究都面临资料问题。在许多场合，问题仅仅是无法获得相关的资料。在另一些场合，从可以获取的资料中计算出来的变量又不正好是想要的变量。在用S.I．C．资料来计算行业结构时常常会碰到这类问题。让我们来看一看出口问题。相对于行业的平均数来说，领先厂商出口得越多，各种行业量度——如有关领先厂商相对产量的发货值——就越会估计偏高。相反，与行业平均数相比，领先厂商进口得越多，这类量度的估计就越会偏低。如果大公司拥有许多工厂并从一家工厂向同行业中另一家工厂发货的话，还会产生另一个问题。大公司通常比较小的公司拥有更多的工厂，而小公司常常只有一家工厂。在这种情况下，由于发货额的重复计算，领先公司就显得占有一个较大的行业份额。

    上面我们已讨论了覆盖率和专业化率。综合地考察这两个比率．我们就可以对不同行业中搜集起来的资料是否恰当作出一个相对准确的估计。遗憾的是，各个行业及领先厂商的专业化率和覆盖率并不都是公布出来的。因此我们无法在分析中确定这些厂商的份额是否代表了它们所在行业产品的实际份额。例如，如果领先厂商的产品专业化率总的说来低于行业平均数的话，那么，集中率将会估计偏高。如果领先厂商的覆盖率总的说来高于行业平均数，也会出现同样的情况。

各种集中率——对它们所含缺陷的一个小结

    在实际计算集中率之前，小结一下前面讨论中提到的各种缺陷是重要的。我们把这些缺陷分别列在下面，尽管不一定按其重要性大小排列。

    1．由于各种集中率建立在全国性的资料基础上，因此它们忽视了地方性的市场势力和集中。

    2．它们忽视了进出口。

    3．它们未考虑到潜在进入者的竞争力量。

    4．在考察市场时，S．I.C．体系反映的经济市场可能是不准确的。

    5. 它们没有反映位次变动。

    6．从集中率无法看出集中率中包含的厂商组的相对规模和相对地位。

    7．它们仅仅刻划了一部分厂商的活功及其规模分布。

    8．在考察市场中的厂商时，它们并不包含这些厂商的特定行为类型。

    9．在计算集中率指数时任意规定厂商数目。

附录：集中率及其趋势

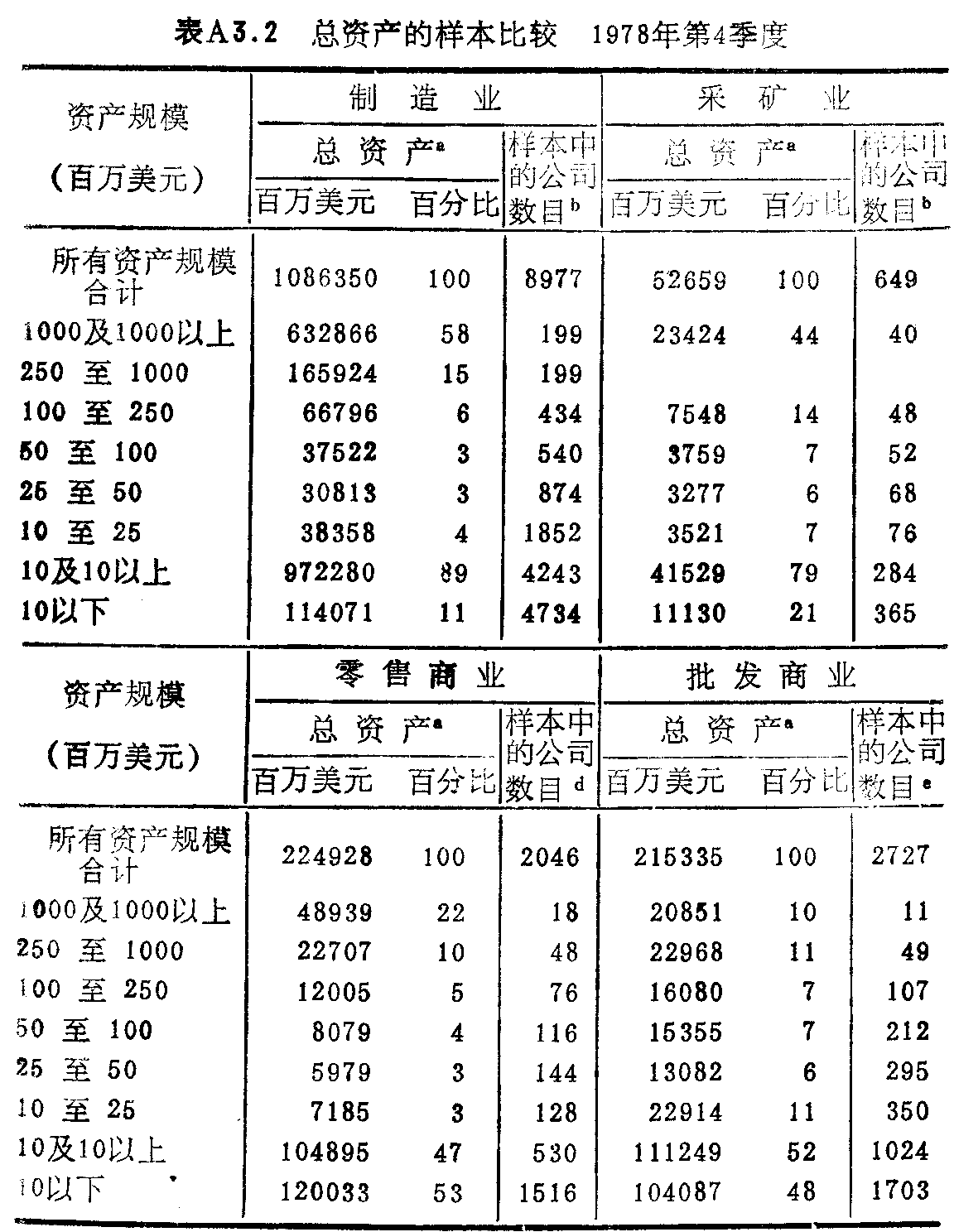
    有关集中的实际量度很多。大部分数值由普查局整理并出版。在表A3．1中，我们给出了1947-1973年中最大50家和最大100家公司所占附加值比重的变化。联邦贸易委员会出版有关行业公布和集中的资料。例如，制造业、采矿业、零售商业和批发商业中各种规模的厂商资产分布见表A3．2。表A3．3列出的是1972年及更早年份中最大4、8、20、50家厂商所占发货值的比重。此外，该表还给出了专业化率和覆盖率。

      表A3．1最大50家及100家制造业公司所占制造业总附加值的份额，1972年及更早年份

年份、公司组别的份额年份、公司组别

    注：每一个特定年份中的最大100家公司都经比较选出，在表的各个年份中分别比较了这些公司在制造业总附加值中的比重，于是该表就记录了一个固定公司组别的集中率在不同年份中的变化情况。若有兼并发生，两家兼并公司中较大的一家仍与以前的公司同样看待。

    a. 总估计数。表中是大概的数字，加总数字与总数不完全相符。

    b．取自一个总数大约为260000的大样本。

    c. 取自一个总数大约为24000的大样本。

    d．取自一个总数大约为525000的大样本。

    e．取自一个总数大约为185000的大样本。

表A3.3一些制造业中最大4、8、20和50家厂商所占总发货值的份额：1972年及更早年份

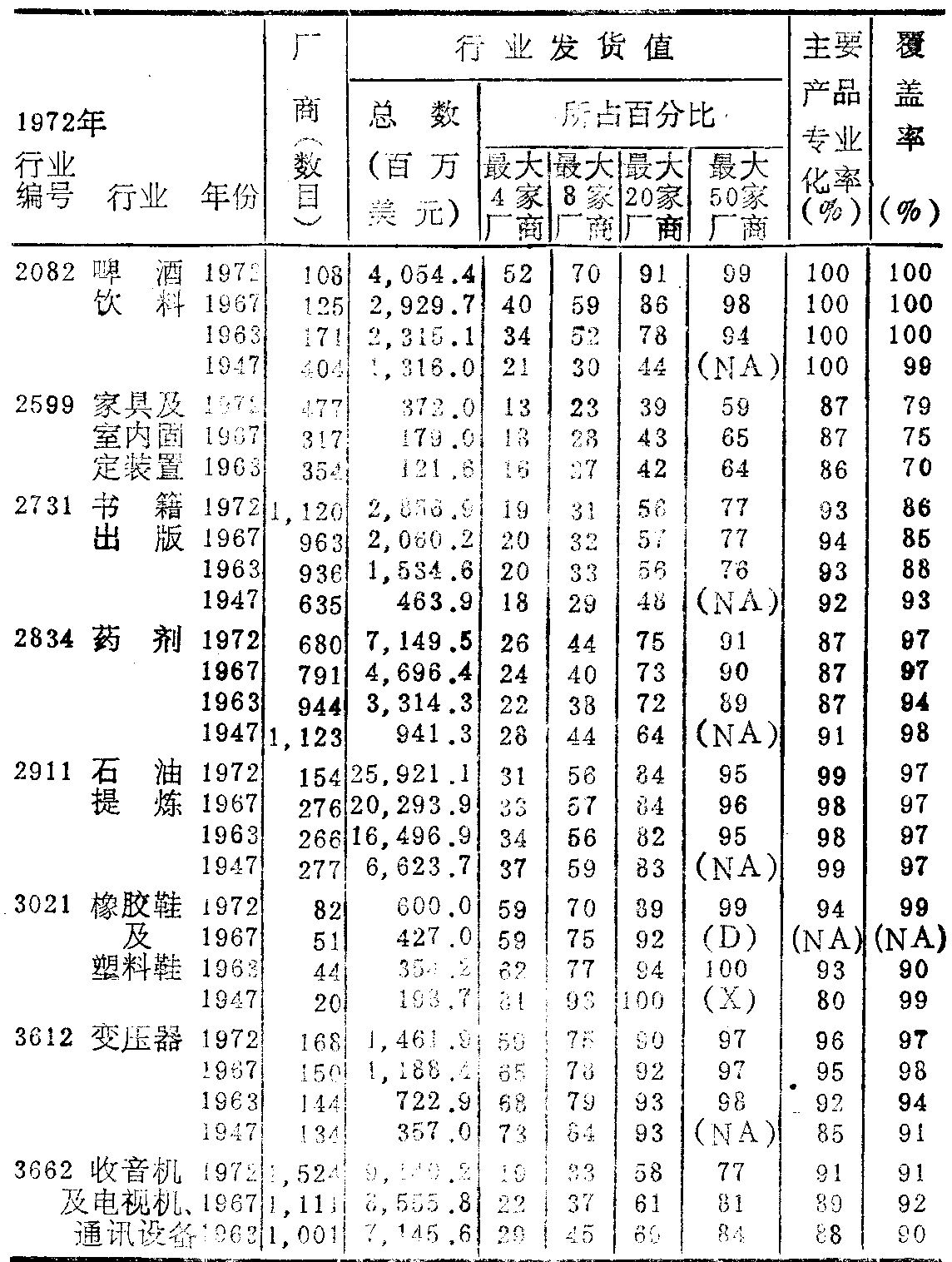
    注：NA表示暂缺。D表示为避免泄漏个别厂商资料而保密。X表示无法应用。