第四章 环境场—视觉组织及其定律

    行为世界的组织和特性。静止过程的一般特征。简洁律。最简单的条件：完全同质的刺激分布。空间组织的某些基本原理。异质刺激：在其他同质场中唯一异质的简单例子——涉及这一例子的两个问题：（1）单位形成；（2）形状问题。作为刺激的点和线：（1）点；（2）线——闭合因素；良好形状的因素；良好的连续；线条图样的三维组织；空间知觉理论的结果：先天论和经验主义；三维空间的组织理论。刺激、线和点的非连续异质：接近性；接近性和等同性；闭合。其他一些异质刺激。组织和简洁律：最小和最大的单一性。来自数量、顺序和意义等观点的组织。

行为世界的组织和特性

    事物的外表由场的组织（field organization）所决定，接近刺激（proximal stimulus）的分布引起了这种场的组织。于是，我们必须把我们的研究用于这种场的组织中去。那么，何种组织对单位形成（unit formation）负责呢？为什么行为空间（behaviouralspace）是三维的呢？组织是如何产生颜色或大小恒常性的呢？这些都是我们必须处理的问题。历史上，这些问题均以随机的顺序得到过研究，每一位实验者选择一个场，在这个场里他碰巧看到一个实际的问题以及解决该问题的一种方法。毋须赘言，我们对许多这样的问题尚无答案，而且，对任何一个问题均无完整的答案。但是，我们现在拥有充分的实验证据，以便为我们的评说提供系统化的程序。我们将以这样一种方式选择我们的材料，它可以使相互依存的主要问题清楚地显示出来。

静止过程的一般特征

    倘若我们的起点更为一般化，则这样一种系统的尝试就会取得更好的成功。因此，在谈论任何一种实验证据以前，我们将问一个问题，即我们是否知道属于一切组织的任何一种组织特性。由于心理的组织是我们的问题，因此我们无法从心理事实中取得我们的答案，可以这样说，心理组织是我们方程式中的未知数。这就意味着，我们必须转向物理学。那么，物理组织，即过程的自发分布，是否显示了我们正在寻找的一般特征呢？

    最大和最小的特性

    当我们转向静止分布（stationary distributions）时，也就是说，时间上的不再变化，我们确实找到了这些特征。静止过程具有某些最大一最小特性（maximum－minimun properties），也就是说，这些过程的一个已知参数（parameter）不仅具有大小，而且具有最大或最小的可能性。我们只需举出几个例子便可使这一点明晰起来：如果我们在同一节电池的两极之间建立起若干电路，那末电流便将自行分布，以便在该系统中产生最小的能量。让我们来举一个只有两部分电路的简单例子。基尔霍夫定律（kirchhoff’ s law）表明了 I1／I2＝ R2／R1，在这一方程式中，I1和I2代表两部分电流的强度（intensities），而R1和R2则代表部分电路中相应的电阻。现在，从数学角度很容易说明，这些电流（即在电阻为R1的电路内电流I1和电阻为R2的电路内电流I2）将产生较少的热量，也就是说，比起电流I1为更大或更小的情况来，比起电流I2为更大或更小的情况来，将产生较少的热量，这是相对于基尔霍夫定律的要求而言的[两种强度之和必须保持不变，因为电路的电流强度仅仅依赖它的电动势（electromotive force）及其全部电阻]。

    另外一个例子是肥皂泡。为什么肥皂泡的形状呈球形呢？在所有固体中，球体的表面积对于特定的体积来说是最小的，或者说，球体的体积对于特定的表面积来说是最大的。因此，肥皂泡解决了一个最大一最小的问题，我们也不难理解个中的原因了。肥皂粒子相互吸引，它们倾向于占据尽可能少的空间，但是，内部的空气压力迫使这些肥皂粒子停留在外面，从而形成这一空气容积的表面膜。它们必须尽可能地形成厚的表面层，如果表面越小，它的厚度就越大，这是以质量的量（amount of mass）保持不变为前提的。与此同时，膜的势能将尽可能小。

    最大量和最小量当然是与占优势的条件相关联的；绝对的最大量是无限的，而最小量则等于零。在我们的上述例子中，所谓条件就是指质量的量，也就是说，肥皂溶液的量和空气容积。在第一个例子中，它是指由电动势和全部电阻产生的整个电路的电流强度。

    现在，我们可以理解有关静态分布的一般观点了，它是我从苛勒（kohler）那里援引过来的：“处于不受时间支配的状态（time－independent states）的一切过程，分布向着最小能量转移”（192年，p．250）。或者，可以这样说，最终的不受时间支配的分布包含能够工作的最小能量。这个观点适用于我们将在后面讨论的整个系统，即在某些条件下，它要求整个系统的一部分吸收最大的能量（参见苛勒，1924年，p．533）。

    于是，我们在物理学中发现了一种静止分布的特征，也即我们已经寻找过的那种特征。如果神经过程是物理过程的话，那末它们必须满足这个条件，不论它们是静止的还是半静止的；我们无法期望在我们的神经系统中找到这样的过程，它们完全不受时间的支配，因为这些条件从不保持绝对的恒定。然而，在短时期内，这些条件的变化在大量的例子中将发生得十分缓慢，以致于为了实用的目的，这些分布在这样的短时期内是静止的；于是，这些过程可以称作准静止的（quasi－stationary），它们可以作为静止过程来处理。这样，我们找到了一切静止的神经组织的一般特征：我们知道，它们必须具有某些特性，仅仅因为它们是静止组织的缘故。就其本身而言，这是一种巨大的收获，但是它并未为我们提供任何一种具体的顿悟（insight），即对心理组织实际性质的顿悟，因为我们没有测量这些过程之能量的工具。我们可以这样说，若以牺牲物理观点的精确性为代价，则在心理组织中，如同占优势的条件所允许的那样，将会发生非多即少的情况。

    质的方面

    我们可以再深入一步。迄今为止，我们的陈述是关于量化方面的，可是，我们的行为环境（behavioural environment）并不反映这种量化；恰恰相反，它是纯质的。那末，我们如何才能在量和质之间架设桥梁呢？关于这个问题，我们已经在第一章中回答过了：量和质并非事件的两个不同特性，而是同一件事件的不同方面。因此，我们可以问：满足量的最小－最大条件的静止的物理过程的质化方面究竟是什么？对于这个问题，不可能取得完全满意的答案，我们没有可以用于一切情形的一般的质化概念。但是，存在一些特例，在这些特例中，静止过程的质化方面开始变得明显起来（苛勒，1920年，pp．257f）。像居里（Curie）和马赫（Mach）等物理学家都曾被自然界中许多稳定形式的对称性（Symmetry）和规律性（regularity）所围困，诸如结晶体就属于此类。于是，居里系统地阐述了下述的主张，“某些对称要素并不存在，这对于任何一种物理过程的发生来说是必要的”；苛勒则系统阐述了这一主张的反题：听任自身处置的一种系统将会在趋向一种不受时间支配的状态中失去其不对称性，并变得更具规律性。

    只要过程得以发生的条件是简单的，则这一主张的措词便是十分清楚的了。但是，当过程得以发生的条件变得不怎么简单时，将会发生什么情况呢？一个非常具有启发性的例子是水滴。当水滴悬于具有同样密度的媒体（medium）中时，它们将是完美的球体；借助固体的支持，球状稍微扁平；当水滴穿过空气时，它们又表现出一种新的形状，尽管这种形状比球状更不简单，却仍然是完全对称的，并满足以下的条件，即水滴的形状使它穿越空气时受到的阻力最小，这样一来，它便可以下落得尽可能地快；换言之，下降的水滴完全是流线型的（streamlined）；它的对称性再次与最大-最小原理相一致。我们在这个例子中看到了一种静止状态如何随着越来越复杂的条件而变得越来越不简单，平衡（equilibrium）状态便是在这些条件下建立起来的。所以，当媒体处于复杂状态时，当媒体以一种复杂的方式使其特性逐点发生变化时，随之而产生的静止分布在某种意义上说便不再是有规律的或对称的，我们就不再拥有概念去描述这类分布的质化方面。概念将不得不是这样的，即普通的对称性将成为特例，只在特别简单的条件下实现。

    尽管我们收获不大，但是我们已经获得了一些东西。我们至少能够选择在简单条件下发生的心理组织，并预言它们具有规律性、对称性和单一性（simplicity）。这一结论是以“心物同型论”（isomorphism）的原理为基础的，根据这一原理，生理过程的特征也就是与之相应的意识过程的特征。

    此外，我们必须记住，始终存在着两种可能性，它们与最小量和最大量相一致；从而发生非多即少的情况。因此，根据这两种可能性，我们的术语——单一性或规律性将具有不同含义。最小事件的单一性将与最大事件的单一性有所区别。至于这两种可能性中哪一种可能性会在每一种具体情形里实现，则依赖于该过程的一般条件。

简洁律

    我们已经得到了一个一般的原理，尽管公认为是有点含糊的原理，但它指导着我们对心物组织（psychophysical organization）进行研究。在我们的研究过程中，我们将使这一原理变得更加具体；我们将习得关于单一性和规律性本身的更多的东西。该原理是由威特海默（Wertheimer）引入的，他称这一原理为简洁律（law  of Pragnanz）。它可以简要地阐述如下：心理组织将总是如占优势的条件所允许的那样“良好”（good）。在这一定义中，“良好”这个术语未被界定。它包括下列特性，例如规律性、对称性、单一性，以及我们在讨论过程中将会遇到的其他一些特性。

最简单的条件：完全同质的刺激分布

    现在，让我们从研究具体的心理组织开始！我们从一个最简单的例子开始我们的阐释，这个例子仅仅在最近才引起心理学家的注意。只有当力的分布在感官表面上绝对同质（homoge-neous）时，这个最简单的例子才得以实现。

    为什么这是一个最简单的条件：不同的传统观点

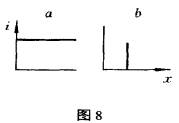
    为什么事物像看上去的那样？这个问题我们在前一章已经讨论过了。为了把这一例子看作是最简单的例子（尽管它看来是理所当然的），我们需要在回答问题时作出剧烈的改变。只要人们期望对我们问题的答案来自局部刺激（local stimulation）结果的调查，那么，另一情形看来便是最简单的了，也就是说，在该情形中，视网膜只有一点受到刺激。实验证据（该证据我们将在后面进行讨论）表明这种假设是错误的。同样的结论直接来自我们的第三个答案。如果知觉便是组织的话，也就是说，一个拓展中的心物过程有赖于整个刺激分布，那么，这种分布的同质性必定是最简单的情形，而不是包含不连续性（discontinuity）的传统情形。我们可以用数学方式来表述这两种刺激，也就是测定视网膜上位置功能的刺激强度。由于视网膜是一个表面，视网膜上的每个点可以按照笛卡尔坐标系（Decartesian system of co-ordinates）而在一个平面上描绘。每个点的强度必须被描绘为这一平面上的一个点，所有强度将存在于一个表面上，它的形状有赖于强度的分布。现在，如果强度是同质的，那么这个表面就将是与xy平面相平行的一个平面，平面上方位置越高，强度也就越大，而且，在距离为零时，与之相应，强度也等于零。相反，如果我们的视网膜只有一点受到刺激，那么我们的表面就不再是一个作为整体的平面了。它的最大部分仍将与xy平面保持一致，但是，在一个点上，对受到刺激的这个点来说，其强度将呈陡峭的上升走势，在下一点上又重新。下降至xy平面。如果我们不想运用透视图的话，我们便只能复制一个有关这些分布的二维截面图。然后，我们可以在横坐标上沿着视网膜的一条线（譬如说，视网膜水平线）测定所有的点和纵坐标上的强度。一般说来，所谓视网膜水平线是指眼睛处于正常位置时通过视觉中心的一根水平线。因此，图8a代表强度i的同质分布，图8b则描绘了只有一点受到刺激时的分布情况。在图8a里面，上方的线表示分布，而在图8b里面，则整个图解均表示分布情况，因为在X轴和i轴上除了该点之外都是一致的。第一幅图与一个完全的平面相一致，而第二幅图与一个具有极性（pole）的平面相一致。那么，当我们的视网膜按照第一幅图形受到中性光（neutral light）刺激时，我们将看见什么？

    中性光的同质分布

    我必须用新的条件来修改一般的问题，这里的新条件是指，光是中性的，因为用这些刺激分布所做的实验采用的便是中性光。我们将在后面就光非中性的情形提供一个假设性陈述。

    产生这种同质刺激的不同的距离刺激

    对我们问题的回答颇为简单：在这些条件下，观察者将会“感到他自己在雾霭般的光线中游泳，光线在不定的距离上变得更加聚集（condensed）起来”［梅茨格（Metzger），1930年，p．13」。让我们考虑一下我们是如何在视网膜的整个区域内产生这种一致的强度分配的；换言之，我们必须使用哪些距离刺激（distantstimuli）以便获得同质的接近刺激（proximal stimulation）。当然，我们可以使我们的被试置于实际的迷雾之中，并对迷雾予以均匀照明，在该情形里，被试的行为场将是地理场的良好代表；看到的雾与实际的雾相一致。即便如此，不断增加的聚集将是属于行为雾（behavioural fog）的特征，而不是属于实际雾的特征。但是，我们可以通过完全不同的手段来产生同样的接近刺激。置于观察者面前的任何一个表面，如果面上的每个点均把同样数量的光送入观察者的眼中，这将满足我们的条件。不论他是位于一个平坦的垂直墙前面，还是位于一个半球的中央，或者身处一片实际的雾中，对他来说不会有什么不同；他将始终看到充斥着空间的迷雾，而不是一个平面。此外，不管面的反照率（albedo）是什么，如果从面上反射的光保持不变，那也不会有什么不同。反照率是反射系数（coefficient of reflection），即用单位面积接受的光量去除以单位面积反射的光量；而反射的光量是投射于单位面积的光的产物和反照率。如果L代表反照率，i代表反射光的强度，I代表投射到单位面积上的光的强度，那末：

L＝i／I，并且i＝IL

    由于没有任何一种表面能将投射于其上的所有光反射出去，因此L始终小于I。如果L与I呈反比的话，则i保持不变。

i＝LI’＝（LP）I/P

    这里的P是指任何正数（positive number）。

    这些条件下的白色恒常性

    因此，在绝对同质的刺激条件下，雾的外表只能依赖i，如果i保持恒常，并且完全不受L的支配，情况必定是这样。换言之，有两个面，一个面比另一个面明亮10倍，但是接受的光照却只有后者的1／10，那么这两个面肯定产生同样的知觉。这意昧着，在这些条件下不可能存在白色恒常性，因为恒常性是指，实际的外表是反照率的一个函数；在正常条件下，一个处于充分光照下的黑色表面像阴影中的一个白色表面一样反射同样多的光，但是这个黑色表面看起来与白色表面并不一样亮，对此问题，我们将在最后一章予以讨论。

    白色和坚持

    如果使用全部同质的刺激，那末就不可能发生任何恒常性，这个否定陈述涉及下面的肯定主张，即一切恒常性预示了刺激的异质性，并为我们提供了解释恒常性的第一条线索。另一方面，这个否定陈述还留给我们一个问题；当两个同质的面以反照率L1和L2接收光照量I1和I2，在L1I1=L2I2时，如果这两个同质面引起了同样的知觉，那么这种知觉将成为什么样子？它们呈白色还是灰色还是黑色？只有当我们知道了外表对i（即反射光的强度）的依赖性以后，我们方才能够回答这个问题。但是，这个函数或多或少还是未知的。我们能够肯定地说的是，这个函数的因变量（dependent variable）即雾的外表，具有几个方面，它们可以作为分离变量（Separate variables）来处理。我们必须至少在它的“白色”和它的“印象”（impressiveness）或“坚持”（insis－tency）之间作出区分。前者意指它与黑白系列成员的相似性，后者意指一种特征，它不仅仅涉及行为目标，而且涉及自我（Ego），即自我和行为目标之间的一种关系（梅茨格，p．20）。早在1896年，G．E．缪勒（Muller）把“印象”界定为“感觉印象用以吸引我们注意的力量”（pp．20f．）。如果这是指一种直接描述的话，那么，看来它与我们文章中的陈述是等同的，我们的陈述取自梅茨格，他也摘引了缪勒的话，而铁钦纳（Titchener）的三个术语更加清楚地带出了目标－自我的关系（object－Ego relation）。当我们引入自我时，我们将讨论与坚持类似的特征，但是，有意义的是，如果我们不是被迫地去提及自我的话，我们甚至无法开始关于环境场的讨论。环境场的特征是一个自我的场，这种自我直接受该场的影响。

    同质刺激强度的效应

    然而，我们必须回到自己的问题上来，即雾的外表和刺激强度的关系问题。由于我们的知识仍然很不完整，因此，我们可以不考虑适应性在这种关系上的效应，这里的所谓适应性，是指一般意义上的暗适应和光适应（dark and light adaptation）。我们可以根据梅茨格在绝对同质刺激条件下取得的结果而得出结论，坚持随强度而变化大于坚持随白色而变化。梅茨格提供了有关场中事件（从绝对的黑暗开始，逐渐明亮起来）的描述。“起初，对观察者来说，它是在沉闷减少的意义上亮起来的，而不是在黑暗减少的意义上亮起来的，观察者感到一种压力的消失，他似乎可以再次自由自在地呼吸了；有些人同时看到了空间的明显扩展。只有到了那时，它才会在黑暗减少的意义上迅速地亮起来，与此同时，充斥空间的色彩也降低了”（p．16）。由于他无法在较高的强度上产生完全同质的刺激分布，因此，我们无法确定被见到的迷雾空间的深度对刺激强度的依赖性，但是，我们看到了刺激的开始，也看到了刺激的第一次增强产生了明显的扩张。这种扩张再次与自我相关；只要注意一下从压力下解脱出来就行了，这种压力恰恰是刺激的首次结果。

    梅茨格的仪器设备

    现在，让我们简要地描述一下梅茨格的仪器设备。观察者坐在经过仔细粉刷的墙的前面，墙的面积为4×4平方米，距离为1．25米。如果观察者直接坐在墙中央的对面，那么这堵墙便不会全部进入观察者的视野，它与水平方向大约200度视角相一致，并与垂直方向的125度视角相一致，而墙的侧面仅仅填满了116度的视角。由于观察者坐在置于房间地板上的一把椅子上，凝视着地板上方约1．5米的一个点，所以，墙壁的维度在任何一个方向上都是不充分的；因此，朝向观察者的两侧必须加到所有的四条边上去，从而使引入的异质尽可能地小。实际上，墙壁和两侧结合在一起的几条边一开始就看不见，或者过了很短的时间就看不见。照明是由一台幻灯机提供的，这台幻灯具有一组特殊结构的透镜。

    微观结构的刺激

    迄今为止报道的结果是从上述仪器中获得的，只要照明强度保持在一定水平以下便可以了。然而，如果明度增强，就会发生某种新的情况。雾就会聚集成规则的曲面，这种曲面从各个侧面将观察者包围起来；它的外表如同天空一般朦胧，而且是与天空相似的，因为其中央也稍稍扁平。雾的边缘的外表距离与正常条件下见到的墙壁边缘的外表距离是大致相同的。如果明度进一步增强，面就笔直地伸展成一个平面，它的外表距离可以十分明确地增加，一直延伸到实际距离以外。

    为什么会出现从充满空间的雾向一个平面转变呢？梅茨格的实验（该实验由于太复杂而不能在这里描述）提供了答案。原因在于粉刷过的表面的“粒子”，或者，根据接近刺激的原理，原因在于下述的事实，即在较高强度的情况下，刺激分布不再完全是同质的，而是具有我们称之为一种微观结构（microstructure）的东西。现在距离刺激物体的微观结构当然是不受明度控制的；为什么接近的微观结构却有赖于明度呢？答案可以在调节（ac－commodation）中找到。由于微观结构，异质如此之小，以致于消失，如果眼睛不是完全聚焦的话，而且，只要明度较低，调节便不再完善——关于这一点，我们将在稍后讨论。我们暂且接受以下事实，即只有当接近刺激不再完全同质时，一个面才可以被看到，而微观结构对产生这一效应来说是充分异质的。

空间组织的某些基本原理

    （1）原始的三维知觉

    这些事实揭示了心物组织的若干基本原理：在最简单的可能的刺激条件下，我们的知觉是三维的（three dimensional）；我们见到，充斥着中性色彩的空间伸展至或多或少不确定的距离，这种距离可能随着刺激强度而变化，尽管这一点尚未确定。

    这一简单的事实废除了对下列问题的若干答案，该问题是：尽管我们的视网膜是二维的（two dimensional），为什么我们能够看到一个三维的空间呢？事实上，贝克莱（Berleley）提供了一个他认为是结论性的证据，即我们不可能“看”到深度，我们的深度知觉（Perception of depth）不可能是感觉的（sensory）。“我认为，大家都同意距离本身无法直接被看到。因为距离是一条线，其一端指向眼睛，它在眼睛的“领地”中仅仅投射一点，该点同样保持不变，不论距离是短是长”（p．162）。

    为使这一论点成为结论性的，就需要两个相互依存的假设。首先，它包含了恒常性假设（constancy hypothesis），认为我们可以通过逐一考查其个别点来调查整个知觉空间。空间未被作为拓展中的过程来处理，而是作为独立的局部过程之和来处理。其次，该论点把刺激分布的维度与刺激结果的维度关联起来。由于视网膜是二维的，因此被见到的空间也必定是二维的。但是，视网膜是大脑三维视觉的界面（boundary surface），建立在这个界面上的力决定了一种扩展至整个三维区的过程。贝克莱的论点仅仅证明了，在某些条件下，客观上位于不同距离的两个点看上去似乎位于同一距离，但是，贝克莱的论点并未证明，这种距离必须是零，因为它没有指明两个物体出现的距离（参见考夫卡，1930年）。

    与贝克莱的论点相似的一种谬论也在感觉心理学的其他领域出现了。经常被提及的这个论点是，如果一个特定的刺激样式具有一定的维度（在这些维度中，该刺激样式可以独立地变化），那末，相应的行为资料也将具有同样数目的维度，而且不会更多。因此，就我们关于光强的双重效应［白色和坚持性（white－ness and insistency）」的陈述而言，人们可能会对一个刺激变量仅与一个知觉变量相对应的问题提出异议，尽管就我所知，该论点尚未用于这一特例。但是，该论点已经用于声学，在声学中，人们可以从纯粹的正弦曲线波（sinnsoidal waves）频率和振幅的双重变异性中得出下列结论，即相应的听觉效果（纯粹的音调）也可能具有这两种属性。由此可见，这一论点的错误是显而易见的。如果使电流通过电解质，那末，电解质便分解，同时产生热，这两种结果——电解质的分解和热的产生均直接有赖于电流的强度。换言之，在原因维度和结果维度之间并不存在逻辑的联系（苛勒，1923年b，p．422）。而且，不论在空间知觉还是在声学中，这一虚假的假设已经对实验和理论产生了决定性影响。一俟我们从自己的解释原理中排除了这种假设，我们就没有必要再去说它了。

    尚不清晰的原始三维空间

    让我们回到三维空间上来。在三维空间的最为原始的形式中，它看上去几乎是同质的；由于雾的浓度随着距离而增加，因此也不必然如此。暂且撇开那点不谈，在整个可见的空间范围内充斥着同样的物质，也就是灰色的雾。我们的空间在正常条件下是多么地不同啊！即使在梅茨格的具有更强明度的实验中，我们的空间也是多么地不同啊！人们在一定的距离内见到一堵白色的墙，白色限于那个平面，处于观察者和墙壁之间的空间看上去并非白色，而是像“纯粹空间”那般透明。于是，我们看到原始空间缺乏正常空间所具有的那种清晰度（articulation）。与此同时，我们也看到，接近刺激的清晰度（仅仅是微观结构）可能产生有关知觉场的更为丰富的清晰度，空的空间（emptyspace）为一彩色面（coloured surface）所终止。由于清晰度要求刺激的异质性，也即对清晰度负有责任的特殊的力，因此我们必须进一步下结论说，同质的三维性，即雾，是一种简单的结果，也即我们的视觉所能看到的最简单的结果。我们被诱使着去说，绝对的同质刺激在神经系统中引起最小的事件；而且，在这些条件下可能很少发生。

    （2）面是组织的强有力产物

    根据前面的讨论，看来，一个面（surface）是一个高度组织的结果，它预示着特殊的力。这些力意味着异质性是一件不言而喻的事。如果一切参数（parameter）都具有恒常值的话，那么在一个系统内便不会发生任何事情。更为特定地说，异质刺激如何在生理场中产生力，这一点已由苛勒于1920年表明了，由于它要求某种物理-化学的详细情节，这里不得不予以省略。

    由于接近刺激的微观结构，这些力产生了空的空间组织和界平面（bounding plane surface）；也就是说，颜色先前曾弥散于整个空间，现在则聚集于由实际的力所支持的一个面上，而且在空间的其余部分中消失。看到一个平面，这似乎是世界上最简单不过的事情了；我们对于使这个平面存在的力是一无所知的，这种简单的知觉是一个高度动力（dynamic）的事情，一俟维持该平面的力受到干扰，该事情就会立即发生变化。强调这一点是重要的，因为人们关于空间知觉的传统陈述（尽管这些人对于我们的知识已经作出了最有价值的贡献），基本上是非动力的，也就是说，是纯粹几何学的，每个点都有它自己的“部位记号”（localsign），而一个面的外表则被认为是与特殊分布的部位记号之和相等的。

    由大脑损伤而引起的力的弱化

    对产生平面的力进行干预也会改变平面的外表。我们已经看到，当刺激异质性的丧失引起力的丧失时将会发生什么情况。但是，我们还可以用另外一种方式对力进行干预。正如我们所见到的那样，实际的心物过程有赖于内部条件和外部条件。让我们来使外部条件保持不变，而仅仅去改变内部条件；也就是说，让我们干预一下我们观察者的大脑，看看究竟会发生什么情况。当然，我们不能为了满足我们的科学好奇心而故意这样做。但是，意外伤害（战争提供了数目惊人的意外伤害的病例）却有助于实现我们的目标。可以毫不夸张地说，一切脑损均影响心物过程的组织，但是，症状表现则依据损伤部位和损伤数量而有所不同［黑德，1926年；戈尔茨坦（Goldstein），1927年］。

    由于我们在人类身上无法进行系统的切除实验，因此，我们必须对偶尔送到我们手上的病例进行研究。现在，正巧有这样一个病例。盖尔布（Gelb）于1920年发现两个病人，他们的组织受到损坏的地方正是我们现在感兴趣的地方。他们根本无法看到真正的面，也就是说，在他们的心物场中发生的色彩过程从未聚集在一个平面上，而是始终具有某种厚度，这种厚度的变化正好与距离刺激的明度相反。因此，如果一个黑色的面看来好像是一个15厘米厚的黑色层，那么，一个白色的面看来就只是2－3厘米厚的一层东西了。同样的道理，在一个白色背景上的黑色圆圈就不会显现在该白色平面上；该黑色圆圈会从白色背景上朝着观察者的方向投射，并离他而去。此外，它还将比我们所见的显得更大一些；如果要求病人指向圆圈的界线，那么，他们会指向圆圈界线以外几个毫米的地方。由此可见构成和塑造图形的力在各个方面均变得更弱，而不仅仅在第三维度上变得更弱。在第三维度中要比在第一维度和第二维度中传播得更远，这当然是由于下列事实，即白色阻止黑色以幅射方向传播，而白色在第三维度中并不产生相似的影响。

    （3）不同的组织阶段

    让我们回到梅茨格的实验上来。在充斥着雾的空间的两个阶段和一个垂直平面的外表之间存在着一个阶段，在这个阶段中，所有颜色均聚集在一个面上，可是，它并不是一个平面，而是一个空“碗”，这个空碗从各方面把观察者包围起来。为了与前面的论点相一致，我们必须下结论说，这样一种曲面（curved sur-face）比一个平面更容易产生，也就是说，它比后者更容易与较弱的力相一致。按照这一解释，进一步的事实是，如果观察者在这只“碗”中滞留时间十分长久，那么该“碗”便开始分解成雾（然而，这雾并不传播到观察者那里，而是在他面前留下清晰的透明层），因为继续暴露于同一种刺激之下将会削弱由刺激施加的力。于是，我们便有了由刺激而产生的组织系列，这些刺激意味着不断增加的有效的力的强度：（1）颜色相等地分布在某个可见的容积（volume）内。这一结果尚未被报道；不论它是否实现，都必定由进一步的实验来确定。（2）颜色分布在整个可见的容积内，但是随着离观察者的距离的不断增加而变浓。（3）颜色限于可见容积的较远一端，该可见容积形成碗状的雾。（4）颜色聚集在雾状表面，该雾状表面像一只碗那般把观察者包围起来。（5）颜色聚集在垂直的平行平面中，该平面具有真正的面的特征（与朦胧性质相反）。第（3）到（5）预示了刺激的异质性，即微观结构；而（2）和（1）则在刺激实际上同质时发生。

    （4）产生和维持行为空间的力

    从上述三点中我们得出以下结论：一切现象空间（phenome－nal space）均为实际有效的力的产物；现象空间如同一只气球，气球的大小依据内部的气压而定，但不可把现象空间比作一只金属球。根据这一观点，即由梅茨格坚持的观点，空间尽可能地变小，尤其在第三维度中。这一观点是以以下事实为基础的，在梅茨格的实验中，空间随增加的明度而扩展，由完全同质的刺激产生的空间，比之普通空间，具有很小的深度。

    这一假设有两个方面必须加以区别，即一般方面和特殊方面。一般方面是把视觉空间解释成动力事件，而不是用几何模式来进行解释，因此，这个方面将可全部纳入我们的系统。特殊方面假定，空间的“膨胀”需要力，因而力越弱则空间将变得越小，力是在特定时刻支持空间的。假设的这个部分看来至少是很可能针对一些特定空间的，梅茨格已经调查过这些空间。但是，在目前这个时刻，我不想超越这些限度对它进行概括。还存在其他可能性，即在其他一些条件下，空间将尽可能地大，以致于需要特殊的力去对它进行约束。要做到这一点，可将界线靠近观察者，或将任何部分物体靠近观察者。

    （5）调节的作用

    现在，让我们来看一下调节的作用（role of accommodation）。在梅茨格的实验中，如果调节得完善，刺激将会异质，并具有微观结构。如果调节得不完善，那么刺激分布将会完全同质。因此，透镜的作用是为更高的清晰过程创造条件，而不是为更低的清晰过程创造条件。如果视觉区将始终产生最小可能的反应是一条普遍规律的话，那末，调节便会以与实际相反的方式运作；它不会使眼睛聚焦于物体上，而是使之置于焦点以外，以便使创造最为同质的刺激分布成为可能。但是，即便在梅茨格实验的极端条件下，调节作用也并非如此；它使得刺激分布尽可能异质，从而使实际过程的分布尽可能清晰起来。我们将在论述场组织和行为之间的关系时（见第八章）重新讨论这个问题。

    （6）同质空间的不稳定性

    同质的空间，甚至空间中很大的同质部分，并不像十分清晰的空间那样稳定。人人都知道，当他处在一间完全黑暗的房间里时，他的眼前会飞舞着光点和光纹。类似的现象也会发生在同质的光照空间中，尽管不是自发发生的；然而，当观察者开始审视其视野，以便检验其是否真的是同质时，他可能会看见光点或云雾状的结构从其视野中飘过。产生这些现象的力导源于神经系统内部，但是，在清晰度良好的正常条件下，整个组织如此稳定，以致于这些力难以产生，即使产生的话，也不能影响牢固建立的结构。

    刺激的时间异质性

    在我们离开异质刺激条件下组织的讨论之前，我们必须排除一种限制，它迄今为止限制了我们的论点。刺激的同质性被理解为空间的同质性。我们只有在空间上的同质刺激持续时，才会关心时间段（period of time）的问题。但是，每一个这样的时间段都有在此之前的时间段和在此之后的时间段，因此，我们筛选出来的时间段必须被认为也处于过去时间和将来时间的承上启下的关系之中。换言之，我们既把我们的同质概念用于空间，也把我们的同质概念用于时间，然后，我们便可以看到，空间上同质刺激的突然开始在时间的刺激分布中引入了异质性；因此，有机体必须有新的作为，而这种新的组织在某些方面依赖先前的组织。我们可以这样认为，完善的同质性将既是时间的又是空间的。如果全部刺激（而不仅仅是视觉刺激）完全是同质的话，那么就根本不会有任何知觉组织，这样的说法是否太大胆了一点呢？当我们身处黑暗并闭上眼睛时，将会发生什么情况呢？起初，我们看到深灰色的空间，几乎并不拓展开去，但是过了一会儿，我们便什么也看不到了。也就是说，视觉世界暂时停止存在了。我不能肯定，当我们身处不完全黑暗但完全同质的空间中时，是否会产生同样的结果。

    彩色的同质空间

    然而，不是因为这种思辨才使我引入这个题目的，而是为了排除我们先前讨论中的一个限制。我们把我们的问题限于中性光的情形。现在，让我们来排除这种限制。在类似梅茨格的实验装置中，当那种投射到墙上的光通过彩色过滤器时，我们将会看到什么东西呢？由于这种实验尚未做过，因此我们并不知道。但是，也有可能作一下无把握的推测。为了简便的缘故，我们假设观察者在实验开始以前发现他本人处于一个正常照明的房间内。接着，同质的彩色照明闯了进来，进入到一个“正常的”空间之中，按照正常的中性原理，将会看到与各自的过滤器颜色相一致的色彩。但是，如果观察者在这个同质的彩色场中逗留的时间十分长久的话，该彩色场会不会看上去继续呈现彩色呢？很可能不会这样；按照我的期盼，它将逐渐变为中性的。为什么我期盼它会有这样的变化，如果真的发生了，其结果意味着什么，这些问题将在后面讨论（见第六章，边码p．256）。我们在这里仅仅提及它至少表明了下列可能性，即持续的同质彩色刺激将会最终产生与中性刺激一样的结果，根据我们的观点，在同质刺激条件下，会发生的东西将是尽可能地少。彩色比中性灰色意味着更多的东西；它是一个附加的事件，一个额外的结果。为了支持这一观点，我将仅仅提及盖尔布的两位病人（也就是前面提到过的两位病人）实际上是色盲的，一个病人是全色盲，另一个病人则是部分色盲，而且，通常情况下，空间组织的障碍往往伴随着颜色视觉的障碍。

    我的假设并没有走得如此之远，以致于声称同质彩色刺激的结果是与同质中性刺激的结果完全一致的。相反，我期望这种结果在物体一自我（object－Ego）的关系中是不同的，这种物体－自我关系在前面曾有所提及。因此，我期盼被试会以不同的心境对同质的红色场和同质的紫色场有所感觉，即便两者均显现为灰色的雾。目前只需指出下述观点便够了，即颜色在其一切方面可能显现为整个组织的一个侧面。

    行为空间不是纯视觉的

    现在，让我们阐释最后一点，以便排除一种误解。倘若认为，在梅茨格的实验中，看到的空间仅仅有赖于视觉刺激的话，那末这样的假设将是错误的。行为空间（behavioural space）是一种更为综合的组织，它除了受视觉之力的支持以外，还受其他的力所支持，值得注意的是，受我们内耳前庭器官中产生的力所支持，还受所谓的深度感觉中产生的力所支持。当然，我们关于行为空间是一种更为综合的组织的说法，不仅对于梅茨格的实验（即由同质的视网膜刺激所产生的空间）来说是站得住脚的，而且对于其他各种视觉空间也是适用的。就功能而言，空间决非纯视觉的。

    对我们的首次实验进行选择是十分容易的，因为刺激的“最简单的”例子可以从对我们问题的界定中推断出来。我们的下一步骤不得不更加武断了。当然，我们可以遵循首次实验为我们提供的方向走下去。我们发现，在不同距离进入各个面的空间构造需要特殊的力，同时，我们也进一步发现，如果这些力仅由另外的同质刺激的微观结构所引起，那么，我们将看到一个构成我们视觉空间之世界的同质的垂直平面。

    由微观结构的同质刺激所产生的平面定位

    现在，我们可以提出的第一个问题是：这个平面将在哪种距离上被看到？遗憾的是，我们尚无充足的实验数据来回答这个问题。梅茨格的实验仅仅证明了下述的情况：可察见的距离在某种程度上有赖于刺激的强度，而且它不一定与“实际”距离一样。这种表述当然只是一种简略。严格地讲，我们无法在实际的数据和现象的数据或行为的数据之间进行比较。当我们为了简便的缘故而使用这一不正确的术语时，我们意指在特定的情境中出现的行为性质与正常的条件下出现的行为性质是不同的。在我们关于同质平面距离的例子中，它可能意指：同质的平面出现在与一个平面不同的距离上，这个平面客观上处于同样的距离，但却形成了一个更加丰富的清晰场的部分。由于我们的行为受制于我们的行为场，这也将意味着，在这些情形中，我们的行为将很难适应地理场，或者说，在行为和行为场之间会存在不一致的情况。更为具体地说，如果我们用一根棒头去触及这个平面，我们开始时不会将棒头推得太远；但是，由于“触及”意味着一种十分明确的经验，这种经验在我们把棒头触及真正的墙壁以前是不会发生的，因此，我们将凭借我们的视觉空间的数据继续移动那根棒头。由此可见，由盖尔布描述的那两位病人，当他们从有轨电车上下来时，容易摔跤，这是因为，鉴于颜色的传播，地面对他们来说显得太近，他们的肌肉也相应地受到刺激。这样一来，真实世界和行为世界之间的不一致便始终可以根据行为来进行描述，而所谓行为，正如我们在第二章中已经见到的那样，既有赖于行为环境，又有赖于地理环境。

    但是，让我们回到我们的问题上来。我们的问题是，在哪种距离上将出现同质平面。即便看到的距离不完全是恒定的，而且在较高的刺激强度下，看到的距离会比实际距离更大些，但是，它毕竟是有限度的。在梅茨格的实验中，眼睛和墙壁最近点之间的距离大约为1．25米。估计的最大距离不会大于该距离的2倍。因此，平面出现的距离范围，如果不是距离本身的话，也是可以充分地加以确定的。那末，它是否有赖于实际距离呢？遗憾的是，我们并不知道，因为在梅茨格的实验中这一点是保持恒定的。于是，存在着这样一种可能性，即行为距离也许有赖于实际距离。当然，实际距离无法直接地影响行为距离。两者之间肯定介入了某种东西。有三种因素可以扮演这种中介角色。第一个因素直接影响刺激：如果距离太大，那末粒子将会变得过于细小，以致于不起作用；微观结构也将消失，刺缴将变成同质，而我们将看到充斥雾的空间。

    因此，第一个因素不能解释在同质墙壁的例子中实际距离和可察见距离之间具有正相关（positive correlation）。于是，剩下来的只有调节和聚合（convergence）这两个因素了。正如我们所见到的那样，调节只有在异质性的地方才有可能。而聚合在我们的实验条件下没有直接的决定作用。我们还无法证明这后一种说法是有根据的，因为我们尚无准备去陈述聚合的直接决定因素（见第八章），不过，聚合和调节在某种程度上是结合在一起的，结果是，当不存在相反的力时，特定的调节将保证某种聚合。

    由于同质墙壁的外表距离将有赖于其实际距离，所以它必须通过调节和聚合的媒介才可以做到这一点。尽管已经进行了许多实验，以确定这两个因素在一个清晰的空间中对物体定位（localization）的影响，但是，根据这些例子为我们的同质平面作出推论仍然是危险的，即便这些实验的结果是单义的（univo－cal）。实际上，进行这样的推论也是不可能的，因为从这些实验中得出的结果是相当矛盾的。我们关于这两个因素的作用尚无确切的知识。但是，我们可以说：假定我们的平面的外表距离有赖于该平面的实际距离，从而也有赖于调节作用和聚合作用的话，那么这种依赖将是一种直接的依赖，而非一种间接的依赖。然而，早期的研究者们却持相反的意见；他们认为，调节和聚合能够影响知觉的数据，只要它们产生它们自己的分离感觉，这些分离感觉以这种或那种方式干预视觉，或者与视觉相熔合。我们无法接受这种观点。一方面，我们并非正常地体验到这类感觉，另一方面，这一理论涉及一种心理化学（mental chemostty），这种东西在我们的体系里没有位置，因为我们的体系是以实际的科学概念为基础的。我们记得的那种直接影响是神经系统本身的状况，这种状况与一定程度的调节和聚合相一致。它需要能量去调节一个附近的物体，并聚合一个附近的物体，在某些限度之内，物体越近则能量越大。这一事实，或者具有类似性质的其他一些事实，可能直接影响空间的组织，正如我们已经看到的那样（请参见边码  p．119），这种空间组织本身是消耗能量的动力过程。嗣后，我们将会看到，这样一种影响（在其存在之处）并不是十分值得考虑的，因此，很可能产生这样的情况，同质平面的现象距离可能十分广泛地有赖于它的实际距离。

异质刺激：在其他同质场中唯一异质的简单例子

    现在，我们必须转向非同质的刺激；一个可能的程度是举出一个简单的例子，在这个例子中，刺激沿一个方向或若干方向逐点发生变化。我们暂且把这个问题搁置一下，留待后面讨论，现在让我们讨论这种情形，即在视网膜上同质刺激分布的范围内，存在一个不同刺激的限定区域。遗憾的是，我们无法在没有限定的情况下处理这种情形。迄今为止，尚未进行过能使这些条件得到满足的实验，即不仅正在闭合（enclosing）的区域，而且已经闭合（enclosed）的区域，都是绝对地同质的。接着，便是由梅茨格进行的实验。墙壁以这样一种强度予以照明，以致于看上去像一只碗。在墙的中央，有一个小方块留着不被照明，由于观察者必须抬起他的双眼，所以，这个未被照明的区域像一个不规则四边形投射于观察者的视网膜上面。观察者在这只“碗”的表面看到了一个黑色的不规则四边形，该“碗”的表面处于这样的区域之内，在那里，显现的不规则四边形与倾斜的头部平行，也就是说，向垂直面倾斜。

    在这种情况下，正在封闭的刺激具有一种微观结构，而已经封闭的刺激则是同质的。然而，后者并不引起充斥空间的雾的知觉；与之相一致的场的这个部分出现在同样的面中，如同与正在闭合的刺激相一致的场的那个部分一样。换言之，这个面由正在闭合的刺激的微观结构所构成，这也决定了小的同质的闭合区域的结果。

    然而，尽管这种结果是有趣的，却并未满足我们关于在另外的同质刺激中一个非连续性（discontinuity）结果的好奇心。因为在这一情形中，面的产生并不由于非连续性，而是由于正在闭合的刺激的微观结构。我们仍需了解最小的非连续性，即使充斥雾的空间的主要影响遭到破坏的非连续性。

    详细说明的条件：场作为一个平面而出现

    由于这一问题尚未得到解答，因此，我们必须限定我们的原始问题。我们将考虑一些情形，在那些情形中，周围的场作为一个平面而出现，不论是由于微观结构，还是由于一般的场清晰度（field articulation），我们将把我们的兴趣集中在由闭合的非连续性在这个平面内产生的结果上面。因此，我们要修改我们关于同质的整个场的假设，以便指一种相对来说大的同质场，而且在其界线以内的某处包含着一种同质的非连续性。实践中，我们将使用一些平面，上面有一些作为距离刺激的点。让我们注视任何一种这样的点，例如，在一张白纸上溅上墨汁而形成的点。于是，我们看到了墨渍。在这个简单的例子中，看来并不包含任何问题。那里有墨渍，而我们也见到了它。但是，我们已经了解到，我们对第一个问题的答案（也就是“为什么事物像看上去的那样”）是错误的。这里，有一个非常实际的问题，它因这类经验的普遍性事实而被隐匿起来了。在我们的新例子中出现的那个墨渍，与在完全同质的刺激条件下充斥雾的空间的外表一样，都是一个问题。看到一个墨渍是一种组织的结果，正如充斥雾的空间是一种组织的结果一样。当然，它是一种不同的组织，我们必须先来描述它的某个方面。

涉及这一例子的两个问题

（1）单位形成

    首先，我们的墨渍是作为一个单位（unit）被看到的，它与场的其余部分相分离（segregated）；其次，墨渍具有形状（shape）。两种描述均具有其理论内涵。为什么墨渍是一个单位？它如何与其周围的事物分离？答案看来是明显的：因为它的颜色不同。如果人们为“因为”一词提供正确含义的话，当然这是正确的答案。然而，颜色的不同与单位的形成不是同一码事。

    单位形成和分离的第一定律

    如果我们把场的一些部分的分离和统一（unification）归之于下列事实，即场的每一部分本身是同质地着色的（coloured），而且与场的环境着色不同，那么这便意味着一条普遍的定律，即单位形成和分离的定律，也就是说，如果接近刺激由若干不同的同质刺激区域所组成，那么接受同一刺激的那些区域将组织成统一的场部分，它们因为刺激之间的差异而与其他的场部分相分离。换言之，刺激的相等产生聚合力（forces of cohesion），而刺激的不等则产生分离力（forces of segregation），如果刺激的不等涉及一种突然变化的话。这些都是真正的动力观点，我们对于墨渍所作的统一和分离的解释，如果采用这种方式来解释的话，就不再是陈辞滥调了。

    统一和分离的力

    具有批判眼光的读者将倾向于要求为我们的动力观点提供某种证明。他会争辩说，这种动力观点是直接从我们理论的基本前提中引伸出来的，但是，他想了解这种动力观点赖以存在的事实基础。让我来满足批评者的要求。我们对心物组织（它不属于物理组织）并无特殊主张，我们将指出，正是这同样的观点却在物理学中站得住脚。为此，让我们来运用苛勒的一个例子（192年，p．138）。如果把油倒入液体之中，两者不相混合，那么，油的表面将在分子的相互作用中明显地保持着，可是，如果该液体具有相同的密度，那末，油便会形成球体，在其他液体中游动。不过，批评家会说，也有一些液体能与油相混和，这样一来，就没有任何一种差异会在物理学中产生这种分离的力。你难道没有在心物组织中获得过任何一种相似的东西吗？我们确实获得过。因此，这一事实比其他事情更能证明：统一和分离实际上是由力产生的动力事件，而不是仅仅由几何模式产生的动力事件。

    利布曼效应

    我要提及由S．利布曼（S．Liebmann）发现和研究的一种效应。一种彩色图形（普通意义上的着色），譬如说一种蓝色图形，在中性的背景上，开始丧失其轮廓和确定性，并简化其形状，如果它是错综复杂的，而且亮度（luminosity）接近于它所在的背景的亮度的话。当这两种亮度相等时，其形状会完全丧失；于是便见到了一种模糊的起伏的污渍，甚至这种污渍形的东西也会在短时间内完全消失。因此，正在闭合的区域和已经闭合的区域之间的刺激差异，如果仅仅是一种颜色的差异，那么至少可以这样说，这种差异比起亮度中的微小差异来，很少有力量在心物场中产生这两个区域的分离。于是，看上去十分相似的两种灰色将会提供十分稳定的组织，如果一种灰色用于图形而另一种灰色用于背景的话，一种深蓝色和看上去十分不同的但却具有同样亮度的灰色将产生不出组织来。这就证明了刺激差异本身并不等于区域的分离；后者不仅是视网膜分布的几何投射，而且是一种动力效应，这种动力效应与某些刺激差异一起发生，而不是与其他一些刺激差异一起发生，当某些十分大的刺激差异不属于对组织来说产生必要的力的那个种类时，它也不可能与这些刺激差异一起出现。

    硬色和软色

    我们可以把两个具有不同亮度的面所产生的生理过程比作不能混和的两种液体，同时，把两个具有相等亮度但颜色不同的面所产生的生理过程比作可以混和的两种液体。利布曼的这一发现经过我们和M．R．哈罗尔（M．R．Harrower）从事的一项研究而被扩展了。我们发现，在这方面，并不是所有的颜色都是相似的，当一种颜色与具有同样亮度的灰色相混和，产生这种灰色的光的波长越短，混和的情况就越好。由此可见，红色是分离得最好的颜色，而蓝色则是分离得最少的颜色。因此，我们引进了硬色和软色（hard and soft colours）之间的区分，红色和黄色属于前者，蓝色和绿色则属于后者。我们也在颜色所拥有的组织能力和明度差异之间作了量的比较（I． pp．159 f．）。观察者坐在两只旋转的具有同样亮度的灰色圆盘前。每一只圆盘均可通过任何一种颜色与背景的灰色相混合，或不同明度的灰色与背景的灰色相混合而产生一个圆环。在一只圆盘上，圆环含有一定量的颜色，譬如说，20度的蓝色，也即一张深蓝色的纸。这样就产生了朦胧圆环的外形。而在另一只圆盘上，由于引进了或淡或深的灰色纸，因此形成的圆环也或明或暗。观察者必须确定，需要多少淡灰色或深灰色才能产生与另一只圆盘上的色环同样明显和清楚的圆环。在所表明的例子中，中性环所需的淡灰色的量是这样的，只要对圆盘的其余部分增加一定程度的白色就行了。

    塔尔博特定律

    让我们简要地解释一下这一程序。根据塔尔博特定律（Talbot’s law），一个旋转的色轮（colour wheel）是由不同的区域组成的，如果它旋转得十分快，以至于完全融合起来，看上去像一只不旋转的色轮，在该轮子上不同区域的颜色同质一致地传播，在数量上与它们的各自区域成比例。换言之，具有若干区域的旋转圆盘相当于一只静止的圆盘，它的色质（quality）是具有不同亮度L1和L2的各区域所包含的色质的平均值。因此，如果a是具有灰色L1那个区域的角度，而B是色质L2那个区域的角度，那末，β＝360－α，旋转圆盘相等于具有亮度L＝αL1十βL2／360=αL1十（360－α）L2的一个静止圆盘。如果我们知道圆盘的亮度以及引入圆环的灰色纸的话，我们就可以从这一公式中计算出圆盘的亮度，我们是按照白色的亮度来表述这些亮度的。如果将白色单位称作亮度1度，那末整个白色圆盘的亮度为360度。

    在我刚才提及的例子中，灰色与蓝色的亮度相等，具有白色单位值47。灰色圆环，其清晰度等于20度的蓝色圆环和340度的灰色圆环，具有的亮度为48，也就是说，它仅仅比其余的亮度多出大约2．l％，而在另一个圆环中，其着色的区域相当于整个圆环的5．2％。

    在另一个实验中，我们运用的绿色并不那么浓，而且比我们的蓝色更淡，数字如下：中性环与8．3％的绿（30度）环同样清晰，该中性环比圆盘的其余区域大约淡3％。利布曼效应，也就是说，使圆环变得模糊不清，在这些条件下并不像我在上面描述它的那样清楚。在这些界线上有其他一些轻微的异质，这些轻微的异质比起颜色差异能够产生的组织来，会产生更好的组织。

    利布曼效应对刺激强度的依赖性

    我们实验的另一个一般的结果是与这一联结相关的。其中，实验装置与前面描述过的装置颇为不同。在一个均质的中性背景中看到一个不规则的彩色图形，该图形的强度和背景都在独立地变化着。在这些条件下，我们发现利布曼效应在低亮度条件下较强，而在高亮度条件下则较弱，或者，换句话说，照明强度越高，统一的力和分离的力也越大。此外，人们发现，白色比起黑色来是一种更硬的颜色，即便当它将同样数量的光投入观察者的眼中时也是如此，该结果是在我和明茨博土（Dr．Mintz）从事的实验中获得的（见第六章）。结果发现，在高亮度的白色背景上，深红色图形实际上根本不会显示利布曼效应；该图形在“重合点”（coincidence point）上不会丧失其清晰度，或者仅仅丧失其清晰度的最模糊痕迹；在这个所谓“重合点”上，图像和背景具有同样的亮度（考夫卡、哈罗尔，Ⅱ）。

    现在，刺激强度增加组织力的这种结果，可能改变我们以梅茨格实验为基础的结论。尽管在他的实验中，更高强度的结果主要是由于微观结构的有效性，这一点是毫无疑问的，但是我们必须考虑这种可能性，即它也有一个直接的结果，以致于一个很明亮的和完全同质的场看来要比一个较不明亮的场更不那么雾茫茫。此外，对盖尔布的两个病人来说，这些结果也解释了为什么在一个平面前面的颜色浓度与平面的白色作相反的变化。

（2）形状问题

    在已经证明了单位形成和分离是一个动力过程（该过程预示了接近刺激中非连续性产生的力）以后，我们必须转向问题的第二个方面。我们的墨渍具有形状。尽管下述的说法是正确的，即形状是由负责单位分离的同样过程产生的，但是，要是认为鉴于这一理由．我们不再需要谈论形状了．这将是错误的。一个简单的演示便可说明，形状引进了一个新问题。让我们来看图9,该图摘自彪勒（Buh-ler，1913年）的研究。这幅图形可以用三种不同形状呈现，两种二维图，一种三维图。该图可以看作（a）像一个具有曲线边缘的正方形；（b）像一张由风吹起的三维的帆；（c）当主要的对称轴从右底斜向左上角成对角线时，像一种风筝。在所有这三种情形里，统一和分离沿着同样的界线发生着；结果，统一和分离本身并没有解释形状。

    证明了的形状现实

    然而，形状并不比单位本身更少真实性。在前面一节中，我们已经证明了单位的现实性；据此，我们现在将证明形状的现实性。我们将通过表明形状具有功能性效应（functional effects）来做到这一点，这种功能性效应既有间接效应，又有直接效应。我们把第一批证明归功于L．哈特曼（L．Hartmann）的一个实验，他研究了形状对临界融合频率（critical fusion frequency）的影响。我们已经简要地提及了以下的事实，一种周期性刺激，如果周期十分短促的话，有着像连续刺激一样的结果，两者之间的关系由塔尔博特定律加以调整。该定律起初是为色轮提供证据的，但是，它也适用于下面的例子，也就是说，当一个光的图形投射到墙壁上面时，一个节光器（episcotister）在幻灯的目标面前旋转。这种节光器可以是一个有孔的圆盘，或者是一只普通的色轮，在该色轮中，一个或多个区域完全消失，当色轮的开口处通过幻灯的面前时，光可以毫无阻碍地通向屏幕。客观上讲，这种情况在屏幕上产生了明和暗之间的交替，而明和暗的周期之比例是由开口区域的大小来决定的。但是，如果这种节光器旋转得十分快，那么便不会有这种交替出现，甚至看不见一点闪烁的迹象；融合已经达到，产生融合的最低速度是临界的融合速度，或者，如果我们计算每个单位时间内不同曝光的数目，那么，我们将建立临界融合频率。这里所描述的实验确实可以由这样一种装置来实施。然而，哈特曼的程序是不同的，它产生了更大的量化差异。哈特曼的程序不是由周期性的黑暗间隔来干预周期性的连续曝光，他只运用了两次曝光；在第一次曝光以前和第二次曝光以后，整个场是完全黑暗的，而且在两次曝光之间，存在一个黑暗的间歇。他使用了舒曼（Schumann）的速示器（tachistoscope），一只在望远镜前旋转的宽边轮子。轮子的边有两个狭长的裂口，裂口的大小不同，而且相互之间的距离也是可以变化的。当这些裂口在望远镜前面经过时，观察者便看到了一个物体暴露在轮子后面，而暴露的时间是由裂口的长度和旋转速度决定的。如果两个裂口带有一个黑色间隔在望远镜和图形之间经过，那么，观察者的经验将有赖于旋转的速度。毋须探讨细节，我仅仅提及两个极端的例子便可以了：如果速度很慢，观察者可以看到该图形两次，而且是在黑暗的间隔之间；然而，如果速度十分快的话，观察者便只能看到一个图形，甚至没有一点闪烁。要确定这种效应发生时的最低速度是容易的，也就是说，所谓的最低速度便是临界的融合速度。在其他许多图形中间，哈特曼也展示了我们的图9，并且指示他的观察者用形状（a）即正方形去看图9，或者用形状（c）即风筝去看图9。观察的结果在表4中加以概括，这些数字提供了轮子旋转的持续时间，以及整个周期的持续时间，也即两次曝光加上它们之间的时间间歇，在这段时间中，一个完整的融合在a＝1／1000秒中发生了。

    表4

    （摘自哈特曼）

    我将用哈特曼用过的另一个图形来补充这些图形。我们既可以把图10看成一个中间有一条很粗的对角钱的正方形，也可以把图10看成两个三角形。

  （在原始的实验中，本图印出的黑色原先是白色，而本图印出的白色原先是黑色）

    这个图形的临界融合周期在表5中提供，该表在一切方面均与前相似。

    在第一个图形中，临界融合周期之间的差异略高于整个周期的10％；在第二个图形中，则略低于整个周期的10％。

    表5

（摘自哈特曼）

    在上述的每一个例子中，较大的数字总是与现象上较简单的图形相一致，这一点是必须记住的。这些数值揭示的重要差别也在质量上得到证实。如果这种临界速度为两种图形中较简单的一种图形所达到，以致于该图形在没有闪烁的情况下被见到，观察者从而被要求转向另一个较不简单的图形，那末，这种形状便会不断地闪烁，直到转轮不断增加速度而使周期进一步缩短为止。第二个图形产生了另一种质的观察，在到达融合以前，如果黑色带是正方形的一部分或两个三角形之间的“死空间”（deadspace），该黑色带看上去就会不同。客观上讲，场的这一特定部分一直是黑色的；即便裂口的通过也不会产生哪怕是最细微的差异。因此，就其本身而言，它根本不该显示闪烁的情况。但是，当它作为两个三角形之间的空间而出现时，这一点才会变得真实，而当图形被看作一个正方形时，它参与了整个图形的闪烁，从而又一次证明了实际上察见的单位的现实。

    在第一个例子中，也就是在彪勒的图形中，两种图形彼此之间的差别仅仅在形状方面，可是，在第二个例子中，差别不仅在形状方面，还在统一方面。因此，第一张表证明了形状的现实，而第二张表则是形状的现实和复合的统一。

    但是，哈特曼还发现了一个比先前描述过的例子更加直接的形状效应。在他的双重曝光和精心阐述的技术等条件下，他发现图形完全融合的明度有赖于它们的形状，而不太明晰的图形比更为明晰的图形显得更暗些。

    形状提供的力

    证明了形状的现实意味着什么呢？我们已经表明，临界融合频率并不是分别涉及每一根神经纤维的事件，而是涉及整个分离的单位，由于与一个特定的单位在一起，它仍然依赖这一单位的形状。两种结果均证明，融合有赖于场的正在融合部分的动力方面，有赖于把它与场的其余部分保持在一起的力以及把它与场的其余部分分开的力，有赖于为它提供形状的力。我们通过间歇刺激而产生的图形与应力（stress）之下的生理区域相一致，这些应力的分布是一个因素，它决定了融合与之发生的容易程度。那末，单位形成和形状之间的关系是什么呢？让我们回到物理学的例子上来，这个例子是在我们关于分离的讨论中选择出来的。我们发现，把油浸入不能与之混和的一种液体中，便会有一些力使油与液体分开，这些力产生自两种媒体的表面之内和两种媒体的表面之间，而同一种表面的力也将使油成形，在特别简单的条件下，这种形状是球形的。这些使油与其他液体分开的力，同时也是使油的粒子保持在一起的力，而且这些力要到最后的形状达到时才会处于一种平衡状态；在此之前，油的表面和内部总有一些拉力改变着油的形状，直到油与周围的液体处于平衡状态为止。如果我们将这一点用于我们知觉形状的问题，我们便必须得出结论：我们的墨渍的形状或任何一种其他图形的形状都是力的结果，这些力不仅将图形与场的其余部分分开，而且使之与场保持平衡状态。因此，在图形内部存在一些力，沿着图形的轮廓也有一些力，这一结论是我们从我们的实验中直接得出的。然而，这一点是基本的；我们在第二章的最后一节中系统阐述了心理学的任务，指出了我们将会采取什么步骤以便发展一种心理学体系。现在，我们所关心的一点便是这第一步的第一部分，也即发现使我们的环境场组织成分离的物体的力。

    这些力的实验证明

    我们已经发现了某些力，现在，我们将补充一些实验证据，以证明组织的物体或单位实际上与场的其余部分在动力上是有所区别的，每一种单位都有其特定的力的分布。我们的第一批例子取自所谓的对比场（field of Contrast）。众所周知，一个小小的灰色场，当它被一个黑色场包围时，比之当它被一个白色场包围时，显得较白一些。这一现象本身将是对我们观点的一种证明，如果以下情况得到证明，也即作为单位而非仅仅作为“黑白事件”之和的黑色场和白色场对这一效应负责，那么，这一现象本身就可证明我们的观点了。这是因为，在那个例子中，处于两种不同环境中的灰色场的不同外表会证明以下的现象，即较大的黑色场和较大的白色场将一些力作用于其中的灰色场，以便改变它们的白色。然而，根据传统上人们所接受的对比理论「这些对比理论在海林的理论（Hering’s theory）中可找到其起源」，对比的效应与场的单位或形状没有任何关系，而仅仅与内部场外面的明度的量和接近性有关。

    传统的对比理论

    按照这一理论，一种白色过程在其整个环境中引起了黑色过程，这种影响的强度依据一种尚不知晓的距离函数而降低。在这一理论的近代形式中，除了在特定的条件下，并未有黑色产生的类似影响，因为并不存在产生黑色的局部刺激。因此，如果一个灰色的内部场（inlying field）在被黑色场包围时，比之该内部场位于具有它自身明度的场内显得较白一些，那么这种情况并不能解释成是黑色背景的白化效应（Whitening effect），而是由于“相等的”灰色场的暗化效应（darkening effect），这里“相等的”这个术语意抬“具有相等的白色”。根据这一观点，两个相等的兴奋将会彼此弱化，每一种兴奋在它的相邻的场内引发黑色过程，从而减少了由射入的光线所产生的白色过程的强度。还有一种现象，处于任何背景上面的灰色小块看来要比灰色大块更淡一些，这一事实可由下述原理来解释，该原理在德文中称作“Bin-nen－Kontrast”，译成英文就是“内部对比”（internal contrast）。即便我们的灰色场被一个深灰场包围起来，该灰色场仍然会因深灰场而被暗化，因为白色过程（随着光的入射而在周围场中仍会被引起）产生了对比，也即内部场中的黑色过程。这一理论的特征在于，对比是一个累积的（summative）和绝对的（absolute）事件；它有赖于兴奋的数量分布和几何分布，有赖于它们的绝对强度，而单位形成和形状既作为两个场的刺激关系被排斥在外，又作为有效因素被排斥在外。

    我们将在后面说明这个理论的第二方面的错误性，也就是它的绝对性特征（character of absoluteness）。此刻，我们必须证明它的累积方面是错误的；因为这种反驳包含了在一个统一的和成形的场部分内运作之力的证据。

    在这样做之前，我必须提请读者注意，从严格的意义上讲，除了明度对比以外还存在色彩对比。在一个较大的红色场内，一个较小的灰色场看上去呈绿色或带有绿色，而在一个绿色场内，一个较小的灰色场则呈红色或带有红色，等等。我还想补充的是，我把正在使用的对比这个术语仅仅作为对已经报道的事实的描述，而并非作为对已经报道的事实的解释。因此，读者在遵循我的论点时，不该将任何理论与“对比”这个术语联结起来，而是判断该论点作为来自事实的结论有何价值。

    反对这个理论的实验证据

    第一个实验是相当陈旧的。威特海默（Wertheimer）在大战开始时告诉了我这一实验，而我在1915年将此刊布（p．40）。大约与此同时，贝努西（Benussi）也发现了这一结果（1916年，p．61n．），并在其著作中指出类似的实验很久以前就由迈耶（Mey－er）在冯特（Wundt）的实验室里完成了，但是，迈耶从这些实验中得出了颇为不同的结论。图11中描绘的形状实际上是威特海默和贝努西图形的结合体。在一个一半是红色一半是绿色的背景上置有一个灰色的圆环。如果我们朴实地注视它，它看上去或多或少呈同质的灰色。现在，我们在红色场和绿色场之间的界线顶端放上一张狭纸条，或者放上一枚针，从而使圆环分成两个半圆。结果，红色场一边的半圆立即会呈现明显的微绿色，而绿色场一边的半圆就会呈现明显的微红色。我们习以将这一实验结果表述如下：由同样的刺激产生的两个分离的图形将看上去彼此不同，在这样的条件下，一个统一的圆形看来仍然是一致的。与该实验有关的理论是什么呢？就刺激方面而言，我们有三个一致的区域处于明确的几何关系之中：也就是一个红色区、一个绿色区和一个灰色区，这三个区域是这样安排的，它使灰色区的一半干扰了红色区，而另一半则干扰了绿色区。根据我们的知识，我们将期望看到三种单位，即一个红色单位、一个绿色单位和一个灰色单位，这种期望在该实验的第一部分得到了满足。接着，我们引进了一种新的异质性，这种异质性把我们的圆环一分为二，成为两个半圆环。于是，发生了某种新的情况；迄今为止无效的情境，也就是位于不同背景中的两个半圆，对于不同的异质进行了干扰，改变了它们自身的颜色性质；换言之，圆环部分与其环境之间刺激的跳跃现在变得有效了。当然，这些刺激的跳跃也存在于实验的第一部分之中，因此，在实验的第二部分中，为两个半圆环提供不同颜色的力肯定也一直存在着。如果整个圆环看起来呈灰色的话，只能是由于这一事实：使圆环结合在一起的聚合力如此之强大，以致于全部或部分地抵御了使该圆环变得异质的其他力的影响。这就把我们引向一个新的组织原理，它是对我们旧原理的转变。新的组织原理认为：场的强有力的统一部分将尽可能像看上去那样一致，也就是说，差不多等于占优势的条件所允许的程度。关于这一观点有许多证据可以提供［富克斯（Fuchs），1923年；考夫卡，1923年；图多尔·哈特（Tudor．Hart），G．M．海德（G．M．Heider）」。

    让我们回到我们的实验上来：我们仍然用不同的方式来表述，也即得出两种力，一种是使圆环一致的力，另一种是使圆环的两部分看来不同的力。当圆环被看作一个完整的圆环时，第一种力更强些，而只有当第一种力变弱时，其他的力才会占上风，从而引起颜色的改变，以及随之而来的形状的改变；这时，人们看到的是两个图形而不是一个图形。在这一组织过程中，稍微的改变便会带出形状的作用。一个圆环是一个完整的平衡的图形，内部并不清晰。可以作这样的假设：使聚合力变得如此强大的特性，导致清晰力继续不起作用。这样的假设似乎有点道理。如果这是正确的解释，那么我们的实验将会产生不同的结果，假如我们用具有两个清晰细分的8字形图形来代替这个圆环的话。如果把这个新图形置于我们的红色场和绿色场中，以致于两种颜色的界线将图形对称地分开，而在这个界线被引进以前，这两部分本该比圆环的两部分看上去彼此之间更为不同。情况确实如此。确实，人们可以从这些实验中获得属于特定形状的聚合力的测量方法。

    内部场的形状决定了它从环境场呈现的对比颜色的数量，这已为G．M．海德的某些实验所表明（p52）。在三个同样大小的大型蓝色场里，她引入了一个小的灰色图形。在第一个蓝色场上面是一个圆，在第二个蓝色场上面是一个环，而在第三个蓝色场上面则是一个较大的圆周，圆周上排列着12个小圆。这些图形的大小是这样的，灰色的总量在所有三个蓝色场中是一样的。现在，根据累积理论，这三种图形应当在不同程度上看上去带点黄色，最后一个图形的黄色最多，而第一个图形的黄色则较少，因为在最后一个图形中，灰色部分与蓝色部分处于密切的接触之中，每一个小圆都被蓝色完全包围起来了，而在第一个图形中，一个相对来说大块的灰色，比较而言是远离蓝色的。然而，事实与这种解释不符，第一个图形，也就是完整的圆，看来最黄，而最后一个图形，则黄色最少。正是那个具有最大聚合力的图形成为最有色彩的图形，这是一种新的迹象，它表明组织程度与着色之间的密切关系。

    当然，下述事实并不互相矛盾，即在威特海默-贝努西的实验中，紧密聚合的图形是着色最少的，可是，在这里，它却是着色最多的，因为在该实验中，由巨大聚合所实施的一致性必须是中性的一致性。而在海德夫人的实验中，一致性和中性颜色之间没有这类联结。

    另一个实验极具独创性，它由威特海默设计，并由本纳利（Benary）实施，后来经过W．H．迈克塞尔（Mikesell）、M．本特利（Bentley）和J．G．詹金斯（J．G．Jenkins）等人的修订而重复做了实验，以一种新方式揭示了组织之力。他们表明，一个（行为的）图形中的力不同于图形界线以外的力。在图12a和b中，有一个小的灰色三角形，它在两个图形中均一致，它位于一个大的黑色三角形（a）上，或者位于一个黑色十字（b）的两臂之间的壁龛处。两个小三角形均在黑色和白色处接界。实际上，小三角形在图a中比之在图b中，它的邻近处有更多的白色，a是从b那里产生的，办法是剪去一些黑色部分，正如图C所示。因此，根据海林的对比理论，小三角形在图a中看上去应该比在图b中更暗一些，可是，实际上在图b中看上去比在图a中更暗一些。原因是显而易见的。从现象上讲，在图a中，三角形位于黑色上，而在图b中，三角形则位于白色上，但是，不论属于黑色还是白色，这个问题完全是一个组织问题，而不是接近刺激的几何分布问题。这是因为，在两种图形的每一种图形中，与之相一致的接近刺激由三个同质的区域构成，这三个同质区域彼此之间都不相同；每一个同质区域在行为空间中产生一个特定的单位，我们已经知道是组织的一种结果。毋庸置疑，这些单位的相互关系是组织过程的产物。因此，对特定的场部分（field－part）的依赖意味着屈从于将该场部分聚合在一起的力，也就是使场部分成为一个整体，并或多或少防御来自场外的力。如果假定这种孤立是完全的，那就错了。本纳利原先的实验，以及后来的实验者所作的贡献，都证明这些力也是有效运作的，其结果，如前所述，已经由本纳利和美国学者用各种不同的图形加以证实了。

    这一实验不仅证明了统一和分离的力的现实，而且也证明了形状的现实。小三角形在一种情形里存在于较大的图形内部，而在另一种情形里则存在于较大的图形外部，这究竟是怎么一回事？答案是：因为在图a中，整个大三角形（小三角形是其中的一部分）是一个充分平衡的良好形状（good form）；单单黑色部分的形状则是较不令人满意的。与此相反的是，在图b中，那个没有小三角形的十字形比之包括小三角形的十字形更是一个良好形状。换言之：组织有赖于最终的形状。在若干几何学上可能的组织中，那个具有最佳形状和最稳定形状的组织实际上将会发生。当然，这不是别的，而是我们的简洁律（law of prag-nance）。

    形状的其他一些直接效应

    我们已经阐释了有关形状的第一个直接效应。现在，我们将引用更多的实验证据，以便证明组织过程中明显的直接效应。在威特海默-本纳利的实验中，这种效应发生在稍微复杂一些的条件之下，也就是比我们开始时的条件复杂一些；在这一实验中，不是具有两个同质场，以及两个同质场之间的质的飞跃，而是具有三个这样的场。为了回到更为简单的情形中去，我们将再次讨论油的例子，该例于假定，油在具有相等的特定密度的液体中呈现球状，如果油与该液体不相混和的话。让我们来问下列问题：如果在不同的物质内，某种物质的球状分布是最稳定的，那么，当一个同质场内出现任何一种形状时，为什么我们看不到一个球体，或至少一个圆呢？（我们可以把球体排斥在外，因为我们假设，在我们的实验中，条件是这样的，即把一切颜色过程集中于一个平面上。）但是，为什么我们看不见一个圆呢？答案十分简单，并将引导我们走向一个有关形状现实的新证明中去。一滴油之所以成为球体，是因为周围液体的结构无力去阻止它屈从于它自己表面上的力和它自己内部的力。就周围的液体而言，任何一种形状将与任何一种其他形状一样理想。然而，当我们用白色表面上的一个不规则黑点去刺激我们的眼睛时，视网膜上建立起来的条件（它使整个过程得以启动，并使其继续发展）确实对过程的最终分布的形状产生影响，这种影响在我们上述的油的球体例子中是不存在的。这是因为，刺激不仅决定了产生于白色之中的黑色的量——如果它确实仅此作为的话，那么，我们应当期望看到一个圆，而不管那个点的形状如何——而且还决定了随之而来的分布的十分明确的空间关系。过程分布的动力形式有赖于刺激分布的几何形式。

    两种组织力量：外力和内力

    在我们的心物情形中，我们有两种力，一种力存在于分布本身的过程之中，而且倾向于在这种分布上面印刻最简单的可能形状，还有一种力存在于这种分布和刺激模式之间，它们限制朝着简单化方向发展的应力。我们把后面这种力称作组织的外力（extermal forces of organization），而把前面这种力称作组织的内力（internal forces of organization），这里所谓的外部和内部，涉及与我们所见到的形状相一致的整个过程的那个部分。

    如果这个假设正确的话，那么，只要这两种力沿同一方向运作，例如，如果我们的点具有圆形，则我们应该期望十分稳定的组织。与之相反，如果这些力处于强烈的冲突之中，那么，由此产生的组织便很少稳定。我们能否证明这些结论呢？

    以这种区分为基础的实验

    这种证明的一般原理是容易识别的。我们必须展示不规则的图形（这些不规则的图形将产生刚才描述过的冲突之力），并观察其结果。在我们挑选的图形和一般的实验条件中，我们可以追求两个目的，使那些阻止稳定组织的力变得很小，或者使它们变得很大。在第一种情形里，我们期望组织的内力变得足够强大，以便去克服这些外力；而在第二种情形里，我们期望不稳定的终极产物（end－products），也就是说，被见到的图形在我们注视它们时发生改变，或者被见到的图形完全未被清晰地组织。实验程序选择了第一种程序方式，并在同样的特定条件得到满足时予以一些偶然的观察。现在，我们就来讨论这些结果。

    外力是强的

    一开始，我们将尽可能密切关注这一刺激情形，我们原先就是以这种刺激情形起步的，也就是说，在较大的同质场中的一点可以在不受时间限制的情况下加以注视。在这种情形里，由视网膜产生的力特别强。如果我们把这些力引入组织内力的激烈冲突中去，将会发生什么情况？为此目的，我们展示了一滴墨渍，尽可能使之产生不规则的轮廓。结果是颇为令人沮丧的。除非我们的墨渍很大，否则它看上去十分清楚和稳定，并具有它的一切不规则性。我们从这一结果中可以得出什么结论呢？首先，它证明了决定之力的强度，为了一个更好的组织而防止较大的位错（dislocation）。毋须任何其他的证据，我们便可以作出这样的假设：这些视网膜的力是唯一运作的力，我们的知觉不过是视网膜刺激模式的几何学投射而已。但是，甚至用不着进一步的知识便可知道，这种假设与观察是颇不一致的。这是因为，当我们看到这样一种不规则的斑点时，我们实际上并不以同样方式看到其整个几何形状。我们首先看到的是一个一般的形状，在轮廓上或多或少地对称，然后看到一些凹进和凸出的东西，这些凹凸形状干扰或改变了这种一般的轮廓；这是一种决不会包含在几何图形中的区分，但却是我们打算寻找的那些组织之力的结果。我承认，单凭这点证据是不足以证明我们的论点的。让我们稍稍深入地分析一下我们的结果，以便看到我们能否发现为什么关于组织的内力的任何一种值得注意的结果未能出现。我们把下述的话作为证据，即外部的组织之力排除了部分的任何一种较大的位错。让我们假设，较小的位错是有可能的。现在，在许多完全不规则的图形中，部分的小型位错不会使它们更加规则起来，因此，没有任何理由说，为什么在这些条件下它们应当发生。但是，这个论点把我们引向一个新的实验：我们把客观图形设计成这种样子，小的位错也可以使图形变得更加规则。当你不带任何批判眼光去看图13，以便把它看作一个整体时，你便会看到一个图形，虽说它不是一个圆，但是也与一个圆差不了多少。实际上它是一个有12只角的多边形，而非一个完全规则的多边形，因为只有4只中心角恰好是30度，其余的角都略为少于或多于30度。这里，将一些部分沿正确方向稍作位错，便会产生一个更加规则的组织，而且这些位错确实在这里发生了；你们看到了一个规则的图形。

    证明这个同样结果的另一种方式是使我们的斑点十分接近于一个正方形，譬如说，两个底角只有89度，而两个顶角则分别为91度。只要人们对它并不十分仔细地审视，便可将这个图形视作一个正方形。

    像上例表示的内部组织之力的有效性的证明，实际上在我们的生活中每时每刻都发生着。我们被矩形的事物所包围，它们在我们看来都呈矩形。甚至当我们不考虑透视畸变（perspec－tive distortion）的事实时，这些例子中的每一个都是手中的一个论点：这是因为，哪一种真正的矩形是数学上确切的矩形呢？通常，比起我们上述的那个图形来，偏差将会相当小，但是偏差存在着，尽管我们仍然看到完美的矩形。现在，下述的论点将会遭到异议，即在我们的日常生活情形里，角度之间的差异如此之小，以致于成为阈下（subliminal）的了。但是，这种异议证明了什么？譬如说有两只角，一只为90度，另一只为90．5度，这两只角从阈下角度上讲有所差异，实际上看来十分相似，但是，这并不意味着它们看起来一定都像直角，它们实际上被看成直角那样；就阈限（threshold）的事实而言，两者看上去至少有点像纯角。因此，这种异议根本不是什么异议，事实上，我们到处见到的矩形是由于下述事实，真正的矩形比起稍稍不确切的矩形来是一个组织得较好的图形，将后者变为前者只需很少的位错。

    但是，我们可以用另一种方式来证明在强烈的外力条件下组织的内力。我们可以不让这些内力产生实际的畸变现象，而使它们完整，并以这种方式与外力发生冲突。图14可被视作一个很不规则的形状，但也可视作两个一致的和对称的形状，其中一个形状部分地倚着另一个形状。在后者的情形里，线条好像在所见的形状中被指明，对于这种所见的形状，没有一种刺激的变化与此一致。因此，由整个黑暗区域的同质刺激所产生的统一之力被分离之力所克服，这些分离之力来自形状完整的图形的统一，两个图形中的每一个图形比起一个具有同质着色的不规则图形来应该说是一个更好的形状。如果转换这两个图形的相对位置，以便使它实际上看来不可能是两个图形，这样做还是容易的。当一个图形比我们的图形更简单时，便可做到这一点，或者当其中之一的突出部分不是一个部分图形的独特部分时，也可以做到这一点。

    外力是弱的

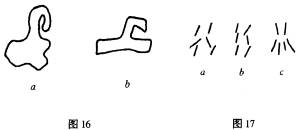
    现在，让我们转到实验中积累起来的证据上来。在这些实验中，外部的组织之力在强度上减弱。为此目的，采用了若干不同的方法：（1）短时展现；（2）低强度；（3）小尺寸；（4）后象（after-images）。结果相同：当不规则图形实际上被展现时，简单的、充分平衡的图形便被看到了。让我们对这些方法中的每一种方法赘言几句。林德曼（Lindemann）接连几次展示一些图形，达20a（sigma），要求被试在每次展示以后把他们所见的东西画出。图15显示了这样的系列图形，最后一个图形是实际展示的，其他几个图形是被试连续作画的再现产品。接下来的两个图形，也就是图16和图17的图形，取自格兰尼特（Granit）1921年的一篇文章。格兰尼特使用了与林德曼相似的方法，但是，他并不要求连续作画。图16的第一个图形是原始的展示图形，另一个图形是由一名  11岁孩子画的图。然而，图17需要我们略加评论。图中的原始图形并不是由单一的异质性产生的单一图形，也就是说不是一个斑点，而是一笔画成的图形。尽管我们将在后面讨论这些条件下发生的组织过程，但我们仍想在目前的讨论中分析一下这个例子和类似的例子（来自其他研究者的例子），这是因为，根据形状简化的观点，这些例子是与其他例子一致的。图17显示了一个原始图形和由两名不同的成人画的再现图形。

    在格兰尼特的例子中，图形的简化如同林德曼的例子。林德曼还使用了另外一种方法，以便证明在短时展现的条件下简单形状所具有的更大的稳定性。林德曼的方法是以不同的时间间隔展示一个圆和一个椭圆的各个部分。在这些条件下，椭圆开始变形，譬如说，变成了橡树果实般的形状，然而，圆却一点也未受影响，或者，当展示时间的差异太大时，圆形被分解为两个部分。

    最后，让我们回顾一下在前面描述过的哈特曼的实验。实验中，一个图形展现两次，两次之间有一个短的时间间隔，而且实验中测量到的整个展现时间正好使该图形呈现为一个整体，没有闪烁。业已发现，当所见的形状是两种可能形状中较简单的一种时，在两种不同形状中所见到的一种刺激模式更容易融合起来。根据我们目前的了解，并与我们先前的结论相一致，我们可以作出解释，即较简单的图形中的内部应力比较不简单的图形中的内部应力小，这种减弱了的内部应力促使两个过程融合成一个过程。

    有关减弱强度的实验早在1900年就由亨普斯特德（Hemp－stead）在铁钦纳（Titchener）的实验室中完成了：把一些图形投放到一块适度照明的屏幕上，一个具有可变开口的节光器在幻灯机和屏幕之间转动。通过逐步增加节光器的开口，图形便变得越来越清晰。如果开口开到最小一档，便什么图形也看不见了；当图形首次开始呈现时，与刺激模式相比，它是明显变形的，变得更加简单，更加对称，具有圆角而非尖角，空隙闭合了，甚至连一般的形状所要求的线条在临时填补的刺激中也不复存在。沃尔法特（Wohlfahrt）曾经用过一些图形，开始时把这些图形的尺寸不断缩小，缩小到看不见的程度，然后再把图形逐渐放大，由此，沃尔法特发现了颇为相似的结果；他强调现象的不稳定性，这种现象的不稳定性好似图形的一种直接可观察的特性；它们看来充满了内力，这些内力在图形内部导致实际的颠簸和跳跃。

    所有这些实验充分证实了我们的期望。如果外部的组织之力较弱，那末内部的组织之力便会十分强大，足以产生相当大的位错，结果导致更为稳定的形状。如果这些图形变得更加稳定的话，则这些力甚至可以产生新的物质过程；新的线条可能被增添上去，对此现象，我们将在稍后加以详细研究。

    现在，让我们转向后象的实验。后象发生在刺激被移去以后，而且，在最简单的情形里，可用同质的面去取代后象。这种情况必须由力来加以解释，它们产生自神经系统中原始发生过程的结果。人们可能会想到可逆的化学反应过程，物质已被分解，分解后的产物现在却重新自行结合起来，通过可逆过程形成了原先的物质。无论如何，这些力完全存在于有机体内部，它们的地位不再受外部能量的影响，从而可以更加自由自在地重新安排自身。由歌德（Goethe）描述的一个古老的观察（人人皆可重复的观察）证实了这样的结论：一个正方形的后象将逐渐失去其尖角，并变得越来越圆。

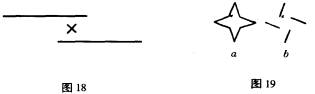
    H·罗斯希尔德（Rothschild）所开展的一些实验是更加有意义的，在这些实验中，一个后象本身的发生有赖于下列事实，即它是否构成一个良好的形状。他没有运用表面图形，而是利用轮廓图形。如果这些轮廓图形是简单的，那么它们便会产生很好的后象；事实上，后象是对原始图形的改进，原因在于所有细微的不规则性均会消失殆尽。另一方面，如果线条并未形成简单的形状，那么后象要么成为较好的形状，要么若干线条根本不会在后象中出现。第一种情况为一个实验所证实，如图18所安排的两根平行线那样。如果两根线出现在后象中，那么它们彼此之间的置换便会大大减弱，结果形成一个不完全菱形的两条边。然而，通常情况下，这两条线并不同时出现，而是彼此交替地出现；这就把我们带到了第二种可能性上面，图19的图形是说明这种可能性的更好例子。图19a提供了一个清晰而又完整的后象，而图19b却并非如此。这里，要么是那根最接近于凝视点的线出现了（在我们图中用X作为标记），要么是两条线交替出现，但是，图19b的四条线却与图19a的四条线相一致。

    这些实验证明了形状的影响，从而也证明了组织的内力在整个组织过程中的运作。

    外力减弱至零

    1．盲点实验

    我们眼睛的解剖结构允许我们再跨前一步，并将外力减至绝对的零。在鼻骨一侧离视网膜中央凹大约13度的地方，有一所谓的“盲点”（blind Spot），该区实际上对光不敏感（如果不是完全不敏感的话）。这个盲点具有稍稍不规则的形状，它的水平范围大约为6度，它的最大的垂直范围则略微大一些。甚至在单眼视觉中，我们的现象空间也不出现空洞（hole），这一事实引起生理学家和心理学家的长期兴趣，而且进行了许多实验，以确定在盲点区域能看到什么东西。有关这些实验的理论解释经常受到含蓄假设的妨碍，这是一种恒常性假设（constancy hypothesis）的特例，即在一组特定的条件下发生的事情也肯定会在所有条件下发生。如果没有这种假设的话，倒是不难把各种实验数据整理出头绪来的。为了我们的目的，只须回顾一下一个实验便够了，那就是沃克曼（VoIkmann，1855年）和威蒂奇（Wittich，1863年）的实验。把一个十字架形状的东西用下列方式呈现，它的中心落在盲点上，而十字形的两臂则伸至视网膜的敏感区里面。在这些条件下，可以看到完整的十字。当十字形的两臂具有不同的颜色时，十字形的中心便以两臂的任何一种颜色显现，主要显现在水平的两臂颜色中。我们在这里举一个很能说明问题的例子，十字形的蓝色垂直臂穿过红色的水平臂，这里，十字形中心呈现红色，尽管客观上它是蓝色的。如果有人转动该十字形，使蓝色臂呈水平状，那么，十字形中心便也显现蓝色。这种水平臂的优势可以得到过度补偿（over compensated），如果有人把垂直臂搞得相对长一点的话。

    那末，这些结果意味着什么？第一个实验表明，心物过程的领域要比受刺激区的领域更大。因此，未受到直接刺激影响的心物场的这个部分所发生的事情，并不有赖于组织的外力，而是完全由组织的内力来决定，这些内力是在直接刺激引起的那些场事件之间获得的。正如图20所示（空白的中央部分与盲点的未兴奋区域相一致），这些场事件并不处于平衡状态，但是，由于以下事实，即没有外力去决定在它们的中心将发生什么事，因此，它们可以而且将会产生一个完整的“十字形组织”，平衡便是在其中获得的。如果十字形的两臂颜色不同，那么，水平臂将决定中心的颜色，因为水平臂部分地落在视网膜区域，这个区域更加中心，功能上更加有效，所以，比起垂直臂来，它将被组织得更好，看上去更清楚。当然，水平臂占支配地位可能有其他原因；尽管如此，这种支配作用也可以通过在其他方面使垂直臂更具印象而得到克服。因此，中心的组织有赖于组织外部有关部分的力；在这一例子中，我们已经把组织的内力孤立起来了。

    2．偏盲实验

    盲点方面的实验有一个欠缺；它的位置如此接近边缘，以致于在盲点邻近地区看到的物体无法清晰地被组织。与中央相比，视网膜边缘的这种劣势是一种组织的劣势，如同其他的组织劣势一样，这种组织的劣势可以与劣势的色彩视觉结合起来。因此，如果我们在视觉中枢开展一些类似的实验，由于视觉中枢没有因为清晰性的缺乏而使观察难以实现，那么，这将产生许多好处。这一可能性是由某些病理性例子提供的，主要由于大脑损伤，致使视野的一半变成全盲。这类偏盲（hemianopsia）的病例已被仔细研究过，这主要归功于波普尔路特（Poppelreuter，1917年），他首先发现，在盲点中观察到的图像的填充（comple－tion），可以很容易地在偏盲者视野的一半盲区中得到证实。我将在这里报告富克斯（Fuchs）的一些实验，他证实了波普尔路特的发现，但是，却为它们提供了一种解释，这种解释在当时（1921年）是全新的，这就是我们在上面提供的关于盲点效应的解释。用偏盲者进行的这些实验，如果它们是去揭示效应的话，必须以短时展现的方式进行，不然的话，病人就会移动眼睛，从而使效应受到破坏。对许多偏盲者来说，尽管不是全体偏盲者，由我们的盲点实验所揭示出来的这种现象也出现了。我们选择的一名病人，他的双眼在视野左侧是看不见东西的，也就是说，对这位病人而言，在其凝视线左方的空间中看不见测试的物体。接着，我们向病人展现一个完整的圆，让其凝视该圆的中心。嗣后，病人报告说，他已经看到一个完整的圆。然而，由于只有实际的圆的右半部与他对圆的知觉有点关系，因此，我们可以移去圆的左半部，效应仍可保持一样。同样的实验也可以用其他图形来重复实施，例如正方形、椭圆形、星形等等。但是，只有用一个八角星才可能使展现的面积少于一半；如果用其他图形的话，那么展现的面积必须超过一半，病人才能看到整体；于是，一个正方形必须展现四分之三的面积，甚至更多。

    现在，这些图形既单一又熟悉。图形的填充可能既由于它们的单一性（simplicity），又由于它们的熟悉性。只有在第一种情况为真时，这些实验才能证明形状对组织的影响；如果熟悉性成为决定因素，那么我们就不得不放弃我们的解释了，至少在这些例子中是如此。然而，富克斯的实验结果明确地作出了有利于第一种选择的决定。比起第一种情况所提到的那些图形来，不论先前是多么熟悉，不论在特定的实验中有过多少练习，非单一性的图形是不可能被填充的。字母，单词，一条狗的图片，一张脸，一只蝴蝶，一个墨水台，以及诸如此类的东西，都以同样负性的成功（negative success）进行了试验。病人认出了这些物体中的每一个物体，但是报告说它们都不是完整的。

    于是，富克斯的这些实验为简单形状中的自发组织提供了完美的证明，一个在当时对格式塔理论有巨大价值的证明。

    我们结论的普遍性：归纳

    在把单位形成和形状作为组织的动力方面确立起来以后，我们现在便可以在新的刺激条件下对它们进行追踪。我们创设的关于两个不同同质区域的条件（一个区域被另一个区域所围住）是一种人为的实验，差不多与我们的完全同质刺激的第一个条件不相上下。然而，这两种人为条件为我们提供了对组织中有效因素的重要顿悟。我们在这里可以提出一个问题，即在这些人为条件下获得的结果能在多大程度上被概括。我们在这里无法恰当地讨论归纳的普遍性问题，也即证明下述的论断是正确的：从有限的例子中得出适用于一切可能例子的结论。但是，我们可以就我们自己的程序说几句话。根据对少量例子的分析，使我们得出结论：分离和单位形成的力产生自两种不同刺激之间的界线上。在我们的例子中，界线将两个同质区域分离开来。那么，在不涉及这种特定条件的情况下来表述我们的结论，这样做是否正确呢？为了解决这个问题，我们首先必须澄清一般观点和特定观点之间的区别是什么。看来它们似乎是同一种观点，唯一的区别在于它们对有效性的要求，第一种观点是一般的，而第二种观点则是特殊的。但是，实际上它们是两种不同的观点而已。第一种观点认为：突然的刺激中断产生了分离的力和统一的力。如果这种说法正确的话，那么，位于这种非连续性任何一边的区域会成为什么东西就无关紧要了。第二种观点与第一种观点相反，它认为：不同性质的同质区域将在它们的界线上产生这些力。那就意味着：突然的刺激中断并不是这些力的充分原因，像第一种观点声称的那样；非连续性加上其他某种东西才是产生这些力的原因。这个问题原先只是一个一般性的问题，现在已转变为一个是否正确的问题。如果第一种观点是正确的，那么它便具有普遍性，如果它是不正确的，那么就不具有普遍性。归纳是产生更多的经验证据的过程，并不在于例子数目的增加（在这些例子中，某种观点是正确的），而是在于通过考查例子b来判断例子a的解释是否正确。再者，根据我们的实验：如果异质区域之间的非连续性并不产生我们在同质区域的实验中已经发现的那些效应，那么，我们原先的结论便是错误的了；如果异质区域之间的非连续性产生了我们在同质区域的实验中已经发现的那些效应，那么我们原先的结论便是正确的，而且具有普遍性。倘若认为后者是真实的，几乎没有这种必要。一滴墨渍并不意味着完全同质的区域，它还有它的统一和形状，因为在它的边界上存在非连续性。

作为刺激的点和线

（1）点

    现在，我们将把我们的原理用于其他一些例子，最后用于那些充斥于我们日常经验的例子。我们从修订我们的上述条件开始，也即一个一致的刺激区域被另一个区域所围住，这里，用不着改变其特征，只要减少封闭区域的大小，首先在一种维度上缩减，接着在两种维度上缩减。第一种程序把我们引向线条，包括直线或曲线；第二种程序则把我们引向一些点。陈旧的理论把这些点作为简单的例子而加以采纳，正如我们先前解释过的那样（参见边码p．110）。现在看来，它是一个特例，将此作为开端可能不好；对于一个被见到的点，尽管从几何学上说这个点可能是一个很小的圆或方块，但是从现象上讲它根本没有任何形状。它只不过是一个点而已。因此，在把点作为我们的标准例子而加以运用时，我们本该忽略知觉中的形状的作用，正像传统的心理学所做的那样。在把点作为一般条件的特例加以考虑时，我们不仅回避了这种误解，而且还获得了对于组织过程的新顿悟。单一的点是不稳定的结构，它们倾向于消失。

    态度

    此外，点的外形通常要求观察者具有明确的态度（attitude）。人们可能会长时间地注视一张白纸，而没有意识到上面有一个点；只有当人们开始产生怀疑，仔细地审视那张纸的时候，他才会发现纸上有一个点。这究竟意味着什么？倘若不抱一种批判态度的话，那么，与那个点相应的刺激的异质性就不足以打破视觉环境中充分界定的单位的同质性。这就需要有一种新的因素，那便是态度，因为态度使那个点得以存在。如果异质性的尺寸更大一点的话，那就会使一个可见的物体跃然纸上，而用不着特定的态度。于是，我们习得了两个新事实。首先，我们发现场组织在某些环境中是有赖于态度的，那就是说，力在环境场中没有其起源，其起源存在于观察者的自我中，这是一种新的标志，说明我们单单研究环境场的任务是有点矫揉造作的，也说明只有当我们研究了把自我包括进其环境中的整个场以后，我们才能完全理解它的构造。

    为什么点是不稳定的

    其次，我们必须提出这样的问题，为什么单个的点是这样的不稳定，为什么它们不可见。假定以此方式来阐述的话，该问题只能得到不合逻辑的回答，正像老一代的心理学家所提供的答案那样，他们会用末被注意的感觉（non－noticed sensations）这一假设来解释这种事实（参见第三章）。但是，这种解释的不确切性在我们的例子中是显而易见的。当我们未能看到一个点时，我们却看到了一个同质的面，也就是说，如果它是白色表面上的一个黑点，那么，当我们没有注意到那个黑点时，我们便只看到白色。对此，“末被注意的感觉”这一假设是无法予以解释的，因为不去注意某种黑色并不等于注意到了某种白色。我们刚才说过，我们的问题阐述得很糟。上述的最后一个观点为我们更好地阐释提供了一条线索。我们不是去问为什么我们看不到某种东西，也就是为什么看不到那个点，而是应当问为什么我们看到了其他的某种东西，也就是看到了同质的表面。为了寻找答案，让我们回到我们前面描述过的威特海默-贝努西的对比实验上来。我们在该实验中看到，一个强有力的统一整体如何抵御了在颜色上使该整体变得异质的那些力量（参见边码PP．134f．）。

    在我们目前的例子中，存在着一种打破表面一致性的力，如果这种力无法产生这种结果，那么失败肯定是由于其他一些更强的力，也就是使统一的区域变得一致的那些力引起的。后面的这些力在整个单一表面的同质着色中有它们的起源，在这个单一的表面中，点仅仅是异质的而已。围绕着这个点，同质过程以闭合的接近性（close proximity）而发生，并以邻近性（contigui-ty）遍及该面的其余部分。我们不久将会看到，相等过程的接近性产生了作为邻近性的同样一些力。因此，在我们的例子中，统一的力一定是很强的，而单一的异质性往往不会强大到在没有附加力量的情况下足以克服这些统一的力。

    我们讨论的一个结论是，看到一个点不是一种原始的成就，而是一种高级的成就。只有在特别发达的系统中，这样一种轻微的异质性才能产生清晰性；在其他一些系统中，这样一种轻微的异质性将产生一种简单的同质场。

（2）线

    现在，让我们来考虑一下线条。普通的线条，不论是直线还是曲线，都被视作是线而非区域。它们虽有形状，但是却缺乏内部和外部之间的差别，鉴于此，它们成为我们一般例子中的另一个特例。从几何学角度讲，我们画的每一根直线都是一个矩形；但是，从心理学上讲，并非如此。另一方面，形状是线的重要特征，对此断语，我们将在稍后用实验证据来证明。

    闭合的轮廓图

    然而，关于线的考虑引进了一个新观点。如果一根线形成了一个闭合的图形，或者几乎是闭合的图形，那么，我们在一个同质背景上便不再仅仅看到一条线，而是看到了由线围起来的面的图形。这个事实如此熟悉，遗憾的是它从未成为特殊研究的课题，这是就我了解的情况而言的。然而，一旦我们剥夺了它的熟悉性的话，它仍是一个令人吃惊的事实。因此，我们要求对下述的说法有一个有效的证明，即由轮廓包围起来的图形是一个与轮廓外面的场不同的实体，轮廓外面的场在其他一切方面产生了同样的刺激。我们拥有一些方法，这些方法有助于确立轮廓图形与其背景之间的差别，但是，这些方法尚未用于我们的问题。我们可以对一个小图形的阈限进行测量（这种小图形产生了我们原始图形的内部轮廓或外部轮廓），测量的方法是把这样的图形投射到有轮廓的面上去，并在幻灯和面之间安放一个节光器，就像亨普斯特德使用的那种实验装置一样（参见边码P143）。如果该小图形要求节光器上面的裂口开得大一些，以便使轮廓内部的东西比轮廓外部的东西更为可见的话，那么，我们便证明封闭区域比之它的环境具有更大的聚合性（cohesive－ness），这就使得在封闭区域上面产生一个新的图像更加困难。遗憾的是，从未做过这样的实验，尽管从两个相似的实验中我们的假设结果似乎是可以预见的。这两个相似的实验，一个是由盖尔布和格兰尼特做的，而另一个则是由格兰尼特做的。

    轮廓图的动力原因

    但是，当我们把这种差别视作实际的差别时，我们的主要问题便出现了。我们想知道这样一些原因，不仅是将轮廓从场的其余部分中分离出来的原因，与此同时，还想了解将封闭图形从其环境分离出来的原因。我们的非连续性原理肯定解释不了这一现象。这是因为，轮廓和画在轮廓上的那个面之间的非连续性，不论在向内的方向还是在向外的方向上都是一样的。根据我们的陈旧原理，我们只能解释为什么我们把线看作线，也就是说，看作与其余部分相分隔的一些单位，但是，当我们看到被一条线围起来的区域时，或者看到由一些线组成的图形时（它们与场的其余部分相分离，而且不是以同样的方式与轮廓相分离），我们所关心的便不是这种情况了。尽管刺激的非连续性仍然具有分离的效果，而且迄今为止与我们的定律相符，但是，这种分离是不对称的。那么，这种不对称的原因是什么？

闭合因素

    遗憾的是，上述问题未被处理。如果仅仅声明一下这是一种疏忽，那就会在读者心中引起怀疑，怀疑我们的一般原理是否有效。因此，我们将设法指出几种因素，它们也许能对这种现象作出解释。我们提出的第一点是这样一个事实，即闭合的或差不多闭合的线或线条图形具有这种特征，而这种特征在不闭合的线条中是缺乏的。这一情况表明，组织过程有赖于其结果的特性，这是严格地符合言简意赅（pragnanz）的普遍规律的。闭合区域似乎是自足的、稳定的组织，这一结论将在后面单独阐释，当然是以特定的实验为基础来阐释。

良好形状的因素

    我们也许会设法找出是否存在闭合的线条或线条图形，这些闭合线条或线条图形比其他线条或图形更易被视作线条。尽管没有做过实验去确定这一点，但我仍然倾向于认为这些差别是存在的，例如，一个圆将更易于被看成是一条线而不是一个三角形，而一个三角形则表现为一个三角形的面，而不像三条线彼此相交于它们的终端点。如果这种说法是正确的话，那么，我们便可以尝试将这一事实与我们的良好形状定律  （law of goodShape）联系起来。作为一条线，圆是最好的图形了。它的每一段都包含了整体原则。可是，三角形却并不如此，三角形中没有一块地方要求按照三角形形成的方式继续下去。恰恰相反，三角形的每一条边的每一部分要求按其自身的方向继续下去，而三角形的三只角实际上却使这种继续方式中断了。因此，可以这样说，作为线段来说，三角形的轮廓并不“简单”。我们可以暂时下这样的结论：三角形的轮廓也是不稳定的。与此对照，三角形的面，尤其当它是等腰三角形或等边三角形时，它的轮廓就是简单的，而且具有对称性。因此，对三角形整个面的分离来说，原因可能在于对称性，它应当由稳定性相伴着。

    简要地说，作为一个暂时性假设，我们提出如下观点：轮廓将图形围起来，而不是作为一条线将自己与面的其余部分相分离，因为这是更好的组织，也是更稳定的组织。

    我们不想以此解释来引进一个新原理。这是因为，我们在此之前已经看到，形状因素作为稳定因素，将组织成一个场，以对抗刺激的非连续性效应。然而，我对我的假设并不感到十分满意。不只因为它缺乏实验证据，而且因为它还不够清楚和明确，它并未陈述沿着轮廓线的实际力量，也未陈述这些力量的不对称作用。

    由线条图样产生的组织

    但是，我们必须让这个问题停留在那里。事实是，区域可以统一起来，也可以通过闭合线条与同质场的其余部分相分离。这一事实有助于我们以新的方式研究形状因素。我们现在将考虑特定的原理，按照这些原理，线条图样（line pattern）产生了组织（线条图样仍是我们一般例子中的一些特例）：该场被分成两个不同的部分，每一个部分本身是同质的或实际上是同质的。现在要讨论的一个图样满足了这一条件；这个场由连续的白色部分（纸张的背景）和连续的黑色部分（一些线条）所组成。所有这些图样是由一个大黑块和移去其中一些黑色而组成的。

    我们的问题是：如果已知某个线条图样，那末我们将看见什么图像？支配这种关系的一般原理是什么？来自柏林实验室的两篇论文包含了丰富的资料，其中一篇论文由戈特沙尔特（Gottschaldt，1926年）所作，是一个不同问题的研究的组成部分，另一篇论文与我们的问题直接有关，由科普费尔曼（Kopfermann）所作，我们将从后者的论文中选择一些例子。

    当我们的线条图样把面的一部分与其他部分分开时，一般不会产生新问题。我们现在要考虑的图样是这样的，其中分开的区域本身包含着一些线条，它们从几何学角度上把分开的区域分成两个或两个以上较小的区域。在这种情况下，我们将见到什么？在较为简单的条件下，当我们不是处理线条图形，而是处理面的图形（surface figures）时，我们也曾偶尔遇到过同样的问题，如果封闭的同质区域具有特定形状的话，那么，它将不是作为一个图形而出现，而是作为两个交迭的图形而出现（见图14，边码p．141）。

    单和双的问题

    让我们把这一例子作为出发点，我们可以提出这样一个问题：一个轮廓图在什么时候被看作是一个在其内部具有一些线条的图形，在什么时候将被看作是两个或两个以上的图形呢？图21和22为上述两种情形提供了例子；在第一个图中，一个人见到一个矩形，中间有一根线穿过，可是在第二个图中，一个人见到两个相连的六边形。原因很清楚：在第一个图中，整个图形比之两个部分的图形来是一个更好的图形，而在第二个图中，情况恰好相反，两个部分的图形比之整个图形来是更好的图形。此外，在第一个图中，矩形的顶边和底边都是连续的直线，可是，如果两个不规则四边形都被看到的话，那么同样的直线就被中断了。

良好的连续

    我们已经遇到了第一个因素；第二个因素意味着（正如我们先前指出过的那样），一条直线与一条虚线相比，前者是一个更加稳定的结构，因此，如果其余情况均相同，组织将以这样一种方式发生，即一根直线继续成为一根直线。我们可以这样来概括：任何曲线将按其自然方式发展，一个圆被看作为一个圆，一个椭圆被看作为一个椭圆，等等。威特海默（1923年）把组织的这一方面称之为“良好连续律”（Law of good continu－ation）。我们在实际的组织中将会遇到许多这方面的例子。这里，我们补充另外一个例子，也就是图23所示的图形，它取自彪勒（Buhler，1913年）的研究，从图中可以看到外力阻止了良好的连续。结果产生了美学上令人不悦的印象，这是因为四个半圆的恰当连续遭到破坏的缘故。

    如果在线条图样中，单（unum）和双（duo）的组织在区域形状和线条连续方面都是同样良好的话，那么两者之中有没有优先者呢？科普费尔曼认为是有的。在有利于单一组织方面，人们优先选择单一的全封闭图形，也即全封闭轮廓。但是，由于科普费尔曼的图形都是这样的，以至于其他一些因素，特别是良好连续的因素．都处于对单一组织的有利方面，结果，她无法证实她的观点。实际上，要产生能够满足我们条件的图样（见图24），如果说不是不可能的话，至少也是极端困难的，即便是这些图样中最好的图样，结果也是模棱两可的。因此，我无法肯定这样一种因素是否存在。

    双重组织

    我们对于单一组织和双重组织的区分，即便我们在双重组织中把看到两个以上图形的情况也包括在内，仍不能适当处理实际组织的多样性问题。一方面，大多数双重形状同时具有单一性质，另一方面，双重形状可能有各种类型。例如，两个毗邻的六边形（见图22）的双重图形，同时也具有一种明确的整体性质，图25也一样，尽管看上去像两个部分相互交迭的三角形，但仍然具有一种明确的整体性质。一个组织的单和双可能彼此和谐一致，确实，这样一种和谐一致可以用无限多样的方式来达到。在一个极端上，我们具有单一的支配性，双重性成了整体的一些完整部分，正如图8所示的那样。可是，在另一极端上，双重性占居支配地位，单一性或多或少成了一些部分的偶然结合，如图26所示，前面举的两个例子（图22和图25）则处于两者之间的某处。双重性本身也可以有各种类型。我们现在来区分两个引人注目的例子：（a）如图22所示，其中两个部分是同等的；（b）如图27所示，一个图形位于另一个图形的“顶上”（on top）。这个例子将在下一章里用更大篇幅来讨论。图28表明了同一种轮廓图形怎样由内部线条来制成，以致于看上去既像单一组织（图28a），又像双重组织（图28b），或者最终成为双重组织（图28c）。良好的形状和连续性解释了所有这些例子。

    经验论者的异议

    我们认为，我们对组织因素的有效性所进行的实验证明是十分充分的，只要我们放弃主张一种旧理论的既得利益的话，这种旧理论要求对一切事实进行解释，可是却不对所有这些不同的组织力量作出解释。我在这里指的是经验主义理论，该理论也许会说：我们在个别的例子中见到这些图形，正如我们以前经常见到的图形那样；我们目前例子中的刺激条件与以前经常重复的例子中的刺激条件十分相似，以致于产生同样的结果。如果对同一种效应提出两种可供选择的理论，那末，必须权衡一下两种理论的相对优点，如果可能的话，还须通过严格的实验，方能在两者之间作出抉择，这是千真万确的。

    现在，让我们来权衡一下经验主义理论关于知觉组织问题的主张。我们来看一下图28的三个系列图形。一位经验主义者也许会说：“我们在图a里面看到一个十边形，它的内部有两条线，我们之所以这样认为，是因为我们经常看到这样一种图形，而不是4个不规则的小图形；在图b里面，我们看到两个长方形，中间夹着一个六边形，我们之所以没把它视作一个十边形，是因为人们经常见到前者的图形；最后，在图C中，由于经常见到方块和长方形，而不是一个十边形，所以，现在便可将此看作方块和长方形了。”这种解释似乎有点道理。不过，在1923年，M．威特海默遇到了这样一种异议，它是由图29那样的图形来组织的，在图29里面，M．威特海默（M．Wertheimer）姓氏的两个首字母，即M和W隐藏在图形里面，苛勒也刊布了若干其他的图形（1925和1929年）。

    对经验论的实验驳斥

    戈特沙尔特于1926年提供了更多的系统证明。在他的实验中，向被试们呈示5个简单的线条图样（即a图样），把这些简单的线条图样投射到一块屏幕上，每一个图样的投射时间为1秒钟，在两个图样的投射之间有3秒钟的时间间隔。然后，告知被试尽可能记住这些图像，以便在后来测试时仍能记得这些图像，并设法把它们画在纸上。在经过一定数量的呈示以后，便向两组被试呈示与第一批图样不同的新图样（即b图样），每个图样呈示2秒钟；然后，告知被试记忆，实验将在嗣后继续进行，与此同时，又向被试呈示一组新图样，仅仅要求他们对这组新图样进行描述，如果这些图片中有什么东西使他们特别印象深刻的话，那么被试只需提一下便可以了。现在，每一个b图样的构成是这样的，即从几何学角度讲，b图中包含着a图，但是，在正常情况下，b图中看不到包含a图的形状。图30提供了一个例子，这是该系列中最难的例子。对于每一个a图来说，会有6个或7个与之对应的b图；例如，对于找们上述图解的a图来说，也有更为容易的b图与之相应（见图刀）。现在，如果经验论是正确的话，那么，看到a图的实践，应当使b图看上去像a加上别的什么东西似的。为了检验这一假设，向3名被试呈示a图，次数为3次，而向另8名被试呈示a图却达到520次。在第一组的3名被试中，有2名被试在所有30次实验中把b图视作新图形，而在第二组的8名被试中，有5名提供了同样的结果。如果把所有被试都归并成一个组，这种实验结果也不会变。

    为了做到这一点，人们必须区分若干不同的可能性：（1）a图将在b图呈现时被立即看到。这种情况在第一组被试的92次实验中仅发生一次，而在第二组被试的242次实验中发生4次。（2）在图形呈示结束时，或者在以后的意像中，被试稍后有了发现。在第一组被试中发生这类情况达5次，而在第二组被试中发生这类情况达3次。（3）被试实际上并未看到a，而是正确地猜测它在那里，这种情况在第一组里没有发生，在第二组里发生5次。（4）被试猜测一个a图，但是却作出了错误的猜测。6）被试只看到b图。

    在表6中，我们用百分比说明（1）－（3）合起来的可能性，其中a图的某种影响能被追踪到；还有（4）和（5）的百分数，其中a图的影响不明显。

    这种假设已遭驳斥。两组数据之间并不存在有意义的差别。此外，在a图的影响是明显的几个例子中，也不可能仅仅是由于经验的缘故；首先，它们并不随着经验的增加而增加，其次，表现出那种影响的被试并不持有完全的中立态度，而是期望再次找到旧的图形，这已为四名被试中两名被试所作的错误猜测所证明。

    表6

（摘自戈特沙尔特）

    结论是，对于为什么我们在一个表示线条图样的形状中见到该线条图样，经验并不作出解释，而是组织的直接力量，例如我们已经分析过的组织的直接力量，才是真正的原因。

    对此结论，我听到了下述一些异议。第一种异议应归功于我的一名学生。该异议认为（与经验主义的原理相一致）我们在b的形状中见到b的图形而不是把它看作a的形状，是因为它们的一些部分是非常熟悉的图形，而且是比a图形更熟悉的图形。由此可见，第二个例子中的正方形和第一个例子中的“格栅”，比起图30a的六边形，在它们的背后有着更多的经验。对于这种异议的第一个回答是，它解释不了为什么在a图的3次重复和520次重复之间的差别并没有对结果产生任何影响。第二种异议是，b图的形状不是在所有情形中都比a图的形状更加熟悉，正如图32所示的例证那样。确实，通常情况下，简单的形状就是熟悉的形状，这种巧合使得经验主义理论变得颇有道理，而且，这种巧合也绝非偶然。如果组织的规律是一些真正的规律，那么我们一定会期望人类活动的产物是简单的，因为人类活动的产物将它们的存在归之于组织过程，这是十分自然的，因此，简单便成为常事。由于单一性和熟悉性之间的这种联系，因此当富克斯证明并不是某些图形的熟悉性，而是它们的单一性构成了图形填充的原因时，这一点具有基本的重要性（参见边码pp．146f．）。我们可以为我们的答复补充第三点：戈特沙尔特设计了一种独特的方法，用来测量在每一个b图中找出a图的困难程度。现在，如果这种异议正确的话，那么，包含最熟悉部分的那些b图应当成为最困难的图形。不过，类似的情形没有一种是正确的。图31比图30更加容易，正方形要比格栅更加熟悉。在戈特沙尔特的b图中，三个最容易的图形之一具有大家都很熟悉的图样。因此，这种貌似聪明的异议无法经受事实的检验。

    另一种异议是这样的：并不存在关于b图的经验，当a图被体验时，它始终处于不同环境之中，因此，人们当然会把“整体情境”（total situation）包括在内。

    “整体情境”

    这一论点之所以貌似有理，是因为“整体情境”这个术语的缘故。但是，事实上该术语并不意指任何东西。在每一个“整体情境”中，有些部分与我们正在研究的特定效应相关，有些部分则与我们正在研究的特定效应无关。于是，“整体情境”这个术语反而使问题变得含糊了。让我们回到前述的图形系列中去，在图28中（见边码p．154），我们曾把经验主义理论用于该图。在这一应用过程中，由于我们没有提及“整体情境”，因此，我们在那些特定的“整体情境”中确实看不到十边形、长方形、六边形和正方形。论争完全集中在以下的事实上，也就是说，我们经常看到这些图形本身，而不是那些图样中未曾显现其形状的图形。看来，经验主义的论争可能不得不如此，否则的话，它将有思辨假设之嫌。例如，如果经验主义的论争声称，在我们系列图样的第一个图样中，我们之所以看到内部有一些线的十边形，是因为我们曾经看到过这种图形或者类似的图形，那么，我们就要询问：“为什么我们在这些刺激条件下单单看到这种形状而不是其他形状呢？”换句话说，如果经验主义者用这种方式来争辩的话，那么，他将犯我们所谓的经验错误。

    最后，产生一些整体情境是相当容易的，这种整体情境是全新的，而且根本不会干扰对a图的辨认。苛勒曾在其著作中（192年，p．210）为这一事实提供了十分确切的论证。图33用一种我们以前经常使用的图样作了同样的说明。如果有些“整体情境”并不干预（或很少干预）特定部分的形状，而另一些“整体情境”则完全抹去特定部分的形状，那么在那些“整体情境”中肯定存在某些特定因素，它们与这种差别有关。在我们的自发组织定律（laws of spontaneous organization）中，我们已经把这些因素筛选出来了。

线条图样的三维组织

    这些定律要比我们迄今为止考虑的二维形状解释更多的东西。在图34的三种图形中，当图a在没有图b和图c的情况下呈现时，它是一个平面图形，一个有着对角线的六边形，或者是一种十字形或星形图形；另一方面，图C看来好似一个立方体，这是就三维角度而言的，而图b则既可以看作二维的，又可看作三维的：也就是说，当把图b看作二维图形时，人们可以看到图35的图形位于一个六边形的上面，而当把图b看作三维图形时，它便成为一个立方体了。实际上，所有这些图形都是同一个用铁丝作边缘的立方体的投射图像，它们中的任何一个都可以构成这样一个立方体的视网膜意像。简单应用我们的定律便会表明，为什么这些不同的投影图像具有这样一些不同的效应。由于图a既具良好形状又具连续性，因此作为一个平面图形，它是完全简单和对称的，而作为一个方方体，那些长的直线则必须断开。对于图C来说，情形恰恰相反，把图C看成平面图形是有点勉强的，因为这种平面图形很不规则，不成其为一个简单的平面图形，所以很难这样去看它。在图b中，力得到更多的平衡，不论是二维方面还是三维方面都是有规可循的。立方体的更大对称性使图b倾向于三维性，而中心垂直线的连续又使它倾向于二维性。鉴于这一原因，图b比图a或图c都要更加模棱两可。科普费尔曼已用其他一些图形发展了这一思想；我也试着去表明为什么经验主义解释是错误的，我运用的论点与我在批驳三维形状的经验主义理论时用过的论点相似（1930年）。

    也许所有的图形中最为简单的证明是下面这个图形了。图36看上去好像是有点变形的长方形。如果你把这页纸对着光，你便可以看到图36呈现两个面，一个面在纸的平面上，而另一个面好像有点翘起或者离你而去。这里，由于将一根线引进了十分简单的图形中，从而产生了这种差别。如果没有这根线，那末这个面便是统一的，有了这根线，这个面便被划分了，而面的各部分关系在三维外表上要比在二维外表上更好些。

空间知觉理论的结果：先天论和经验主义

    这些实验把深度知觉理论（the theory of depth perception）十分清楚地揭示出来了。像立方体那样的图形的三维方面，以及其他一些透视图形，通常是由经验来解释的。甚至先天论者（nativists）也承认，深度感觉是存在的，它由视网膜刺激的不一致而引起，这种视网膜刺激的不一致就是视差（parallax）。先天论者把这一点仅仅视作一个微不足道的基础，在此基础上，我们的三维空间结构，正如我们实际上知觉的三维空间结构那样，是由经验创造出来的。在经验对我们的空间知觉所作出的巨大贡献这一问题上，先天论者和经验主义者之间并不矛盾，唯一的差异在于，经验主义者否认任何一种原始的深度知觉，而先天论者却接受深度知觉，并把它视作其余知觉的基础。美国心理学中的机能（functional）观点已经接受这种现状，但是又对其理论意义的模糊之处作了补充。伍德沃思（Woodworth）谈到了“距离的信号”（signs of distance），这些信号在“三维空间的视觉中一起得到运用”（P．400）。当大多数信号被习得以后，也就是说，有了经验的结果以后，伍德沃思认为“某个距离信号，也许是双目信号，很有可能不必学习”。这种“机能主义者”的深度知觉理论显然是解释性理论的一个例子，关于这种解释性理论，我们已经在本书第三章予以驳斥了。它所增加的模糊性来自“信号”概念。因为我们必须要问信号是什么，以及含义何在。这两者是否都在直接经验中被提供呢？如果确实如此，那么双目信号是什么？如果不是如此，那么我们究竟有什么权利使它们中的一个（例如信号）实体化为经验的一部分和一个符号？

三维空间的组织理论

    针对所有这些理论，我们的假设认为，三维形状在方式上与二维形状一样，也是组织问题，而且有赖于同样的定律。我们远未否定双目视差作为三维原因的重要性，但是，正如我们后面将要表明的那样，我们认为，原因在于组织之力，这些组织之力既可能与其他组织之力合作，也可能与之发生冲突。我在否定经验对深度产生的影响方面还应当格外小心。在我们了解经验意味着什么之前，经验的引入并不具有任何解释价值；只有当我们把经验作为组织本身的一个过程来加以理解时，它方才对我们目前的问题有所帮助。

    组织之力和双目视差

    此时此刻，我们的主要观点是，除了双目视差以外，还有其他一些三维组织的力量，这些力量可能比双目现差这一因素还要强大一些。对此有两个证据：第一个证据包含在我们上述的一切实验之中，其中二维图形看上去像三维图形。因为在所有这些例子中，双目视差的缺乏是把视觉过程组织在一个平面上的一种力量。如果任何一种视差都具有正的或负的深度值的话，那么，视差为零也就等于深度值为零；那就是说，所见的场的一切部分，在没有视差的情况下，应当出现在一个平面上。对我们的一切图形来说，其双目视差值为零，因此，如果这些图形被视作三维图形的话，那么该事实就说明了其他一些组织之力的强度。这些力量不仅克服了视差的缺乏，而且还克服了倾向于在一个平面上进行组织的其他一些条件的缺乏，这些图形所处的那页纸作为一个平面而有力地被组织，这些线条以某种方式从属于这个平面。然而，它们却产生了三维效果。在我们的所有例子中，都发生了二维力量和三维力量的冲突。如果排除这些二维的力量，三维效果应当会强大起来。这一简单的推论是正确的，它已为众所周知的事实所证明，即当一个人闭起一只眼睛，然后去看透视图形时，透视图形便显得更为三维的了。然而，有一个事实也经常被提及，一个透视图形，即便用单眼去看，也不及用双目视差的体视镜（stereoscope）去看时所产生的那种深度印象来得生动。如果我们的假设是正确的话，这种情况必然会这样，因为在体视镜中，视差的三维力量与组织的其他一些三维力量合作；代替力量之间冲突的是，体视镜的视觉引入了相互强化。

    双目视差可为其他组织之力所克服的第二个证明是由科普费尔曼的特定实验所提供的。在这些实验中，线条图样的不同部分以不同距离被客观呈现，办法是把这些线条图样画在玻璃板上，玻璃板以2厘米的间隔距离一块隔一块地插在匣子里。观察者朝匣子里面看，并描述他所见到的东西。如果每一块玻璃板上的图样与其他玻璃板上的图样没有关联，那么，图像便始终在它们正确的相关距离中被见到。但是，如果不同平面上的图样组成一种共同图样的话，那么，这种图样将有赖于我们所知道的组织之力。如果这种力的运作与那些由于视差而产生的力的运作处于同一方向，那么，正确的深度将被见到，否则的话，这一结果将有赖于各种力量的相对强度。在科普费尔曼的实验中，图样是这样的，即内部的组织之力比视差更强大。我们提供三个例子：在图37中，a和b是两个幻灯片，一个接着另一个呈现在观察者面前，c是实际上看到的图形。图形的单一性破坏了深度效果。在图38中，从几何学角度讲与前面的图37差别不大，因此，产生的图形统一性较差；甚至作为一个平面图，它将导致双重的组织，而不是单一的组织。相应而言，这两个部分是一前一后地被看到的。最后是图39的三个图样a、b、c，它们始终被看作一个立方体d，也就是说，看作一个三维物体，该立方体的基础由线条1、2、3、4、5组成，它们分布在所有三块玻璃板上。

    深度的“初级”和“次级”标准

    三维理论作为一种特定的组织形式，是与实验事实相一致的。三维理论要求抛弃初级的（primary）也即“先天的”标准和次级的（secondary）也即“经验的”标准之间的差异，以便有利于组织的外力和内力理论。所有这些传统的次级标准，像形状的重迭、阴影、清晰度的缺乏，等等，必须被解释为组织因素，而不是凭其自身的头衔被解释为经验的项目，即带有特定含义的经验项目。这里，我们将仅仅指出，即便在图40那样的图样中（它是经验主义影响的一个典型例子，而且按图式的角度来说，这种图形与我们从远处的山岳中获得的印象是一致的），我们仍必须根据直接组织来找到它的解释。我们在现实中看到，而且在某种程度上也从图40中看到，在较近的山岳后面是部分地被遮掩的群山，尽管双目视差不起任何作用，因为在真实山岳的例子中，距离实在太大，以致于视差不起作用。

    我们的讨论使我们回到了本章的开头。在本章的开头处，我们讨论了贝克莱的论点，他反对深度视觉的可能性。现在，我们已经熟悉了一组新的事实，可以用来支持我们的批评。先前，我们看到，在没有刺激的异质所产生的强制力量的情况下，视野中的颜色将自行分布在所有三个维度中；现在，我们看到，组织的内力也可以产生三维的形状，而不是二维的形状。第二步实际上是伴随着第一步而发生的。这种情形并不意味着所有影响同质地填补的空间的一切力量之分布将会把它转化为一个平面。有些分布将会做到这一点，而其他一些分布将会把它转化为三维物体。   

刺激、线和点的非连续异质

    现在，我们将在我们的讨论中包括这样一些图样，它们不再是连续的线和点。这些东西将为我们提供两个组织原则的证明，这两个组织原则我们已经提到过，也就是接近性（Proximity）和闭合（closure）。为了便于充分讨论，读者应当转向威特海默的原文（1923年）和苛勒的文章（1925，1930年）。

接近性

    接近性的因素是很容易证明的。在图41和图42的图形中，圆点和线条形成对子，在这些对子中，接近的圆点和线条自发地联合起来。确实，人们也可以任意地看其他的对子，尤其是当距离的差别不是太大时。但是，在同一时间内看到的对子不可能超过一个或二个，这样的对子越多，同时看到远距离的对子就越困难，而其他一些对子则随着对子间增加而获得了稳定性。此外，接近性是一个相对的术语，这是明白无误的；同样的距离，在一个图样中可能是对子内的距离，而在另一个图样中则可能成为对子间的距离。当然，这一定律也是有限制的；当距离太大时，便不会发生任何统一，对子内距离越小，对子便越稳定。

接近性和等同性

    然而，若要系统地阐述接近性定律也不是一件易事。迄今为止，我们只不过证明了，当场包含了若干相等部分时，相等部分中具有更大接近性的一些部分将组织成较高的单位（对子）。这种组织必须被视作与一个同质点的组织同样真实的组织。正如我们用实际的力量对后者作出解释一样（这些实际的力量将一致的区域结合在一起，并将该区域与场的其余部分相分离），我们必须把我们的组群形式视作是由于组群成员之间吸引的实际力量。这不只是一种假设，也不只是一个名称，因为这些力具有可以证明的效果，正如我们以后将会看到的那样，当我们研究有机体对场内的这些力进行反应时，我们可以看到这些力具有可以证明的效果。

    然而，我们的接近性定律迄今为止有赖于接近中的一些部分的等同性（equalty）。即便具有一定的限度，它仍是十分重要的。但是，我们将设法了解，我们能在超越这一限度多大的程度上对它进行概括。在图43a中，该原理仍对归并（grouping）起决定作用。我们看到的归并对子由一条蓝线和一条红线组成，而不是由两条蓝线和两条红线分别组成。

    但是，在图43b中，该结果值得怀疑。因为图43b的图样是更加模棱两可的。我们可以看到接近部分的归并和相等部分的归并。前者（接近部分的归并）看来略占优势，至少，我可以在这些归并中相当容易地看到所有的线，可是在后者（相等部分的归并）中，我倾向于既丢掉了直线，又丢掉了曲线。因此，尽管接近性看来仍支配着等同性，但是，这种优势已经消失，这应归功于我们所引入的一种新差别，也就是说，形状对颜色。我们发现，形状的等同比起颜色的等同来是一个更强的组织因素。在图43c中，两种因素结合起来了，现在，等同性显然超过了接近性，那些对子由相等的线形成，而不是由接近的线形成。在这三种图形中，相对距离犹如1－3。对这些因素的相对强度进行测量是可能的，正如威特海默已经揭示的那样，通过改变这些相对的距离来对这些因素的相对强度进行测量是可能的。如果我们使它们都相等，我们便把等同因素孤立起来了。这种情况在图43的d和e里面都做到了，在这两幅图中，由于形状的差别，e比d更加稳定和更少模棱两可，而d仅仅在颜色上有差别。

    这一讨论似乎要求对接近性定律和等同性定律作如下的系统阐述：场内的两个部分将按照它们的接近程度和等同程度彼此吸引。如果这种说法正确的话，如果接近性和等同性这两个因素中任何一个因素的值为零的话，那就不会发生吸引，从而也不会发生归并。对于接近性来说，这是容易证明的，因为接近的程度，或者它的对立面，也即距离，可以容易地予以量的改变。我们只要将两个场的部分彼此完全分离，吸引之力将会消失，至少就一切实践的目的而言，吸引之力将消失。可是，由于等同程度还不可能被测量，因此也不可能从实验角度去确定当两个场部分完全不同时是否会发生任何归并。然而，我们可以对后一种说法加以限定。分离的部分不会与背景归并在一起；所有的归并在背景上的图像之间发生。因此，在那个意义上说，也就是作为图像来说，如果归并出现，那么就一定存在等同性。这就为等同性这个术语提供了十分重要的判据。至少，迄今为止，等同性与接近性具有同样的立足点；在这个意义上说，没有等同性便没有归并，正像没有接近性便没有归并一样。

    这一论争的目的在于声称，单凭接近性，或者说单凭任何一类事件之间的接近性，并不产生组织之力，力的产生和力的强度有赖于接近状态中的那些过程。上述句子的后一部分已经由我们的上述例证所证明：处于恒常接近条件下的组织有赖于等同性程度，有赖于组织中过程之间的差别。上述句子的前一部分（即单凭接近性不是充足条件）也是正确的，它可以导源于图形一背景（figure－ground）的清晰度。在下一章中，我们将用较大篇幅来讨论图形一背景的清晰度。如果单是接近性成为组织原因的话，我们便与我们在物理学中了解的组织知识发生矛盾。“无论何处，只要A和B在物理学中彼此相关，人们便会发现，其效果有赖于A和B彼此相关中的特性”（苛勒，1929年，p.180）。于是，两个物体按照它们的质量而相互吸引，而且，它们越是接近，则吸引力越大，但是，两个物体也可能在相互之间并不施加任何电力（electric forces）的情况下彼此接近，如果这两个物体在电学上是中性的话。因此，在我们的心物组织中，当两个异质部分由于接近性而形成一个对子时，它们一定在某个方面是等同的，从而能够彼此产生影响。

（实心=红色，影线=蓝色，参见边码p．165注10）

    实际上，我们可以单单通过接近性而将任何一类部分结合在一个组群中，假定这些部分完全可以从其他部分中分离出来的话。我们的图44提供了一个例子。但是，这并不意味着，单凭接近性能将任何东西都集合在一起，而是这些部分具有作为部分的共同特性，这些共同特性解释了这些部分相互作用的原因。

    让我们对接近性和等同性作最后的说明。在图43（a－e）中，可供选择的归并和使形状得以产生的接近性等同，而从任何一种归并中产生的整个图形又是有规则的和一致的。但是，当结果不是有规则的或简单的图形时，接近性和等同性又将如何运作，这个问题尚未进行过研究。像在许多其他方面一样，我们在这一方面的知识仍然不够完整。

闭合

    让我们现在转向闭合（closure）。在前面的讨论中（见边码P．151），我们曾主张，闭合区比不闭合区更加稳定，从而也更容易产生。我们将通过与接近性因素和良好连续性因素相对的闭合组织来证明这一点。图45引自苛勒（1929年）的研究，它是关于闭合组织不考虑接近性因素的一个例证。从占支配的角度而言，并不是那些最接近的垂直线形成对子，而是那些闭合空间形成对子。尽管在图45中，闭合空间的内部距离（两根垂线之间的距离）为两根接近垂线之间距离的三倍，此外，两根短斜线的端间距离与两根接近垂线之间的距离正好相等。而且．在图46里面，也包含图46a的A、B、C、D四个部分。但是，在图a中，按照良好连续因素的原则，B是A的连续，D是C的连续，可是在图b中，两个闭合区都表现为次级整体（subwholes），以致于A不再由B连续，C也不再由D连续。闭合作用并不总是战胜良好的连续，这是由威特海默论文中的若干图像所说明的。关于这篇论文，我在这里省略了，不过，我想证明闭合原则的效用。

    我从点子图中选取了一个例子，用以说明并非所有的闭合作用都同样地好，与此同时也证明了单位形成和形状是组织的两个不同方面。在图47所呈现的两个图形中，b是一个熟悉的图形，使人回忆起北斗七星的犁状星座，而前者看上去则完全是新的。这两个图形由赫兹（Hertz）以不同方式联结了七个点而构成。其中图b的联结方式是我们在天空中常见的星座，而图a的联结方式，尽管在某种意义上说是较为简单的，因为它产生了单一的闭合图形，然而没有人见过这种图形，原因是这个闭合图形十分不规则，而图b的闭合部分却十分简单。

其他一些异质刺激

    我们将通过考虑一些不太人为的刺激条件来结束这场讨论。通常，既非完全同质的分布引发整个刺激模式，又非不同的同质区域构成了整个刺激模式。一般说来，位于刺激发生的跳跃之间的区域，其本身并不同质。关于这种异质性，我们考虑了两个特例。最简单的例子是那样一种异质性，在该异质之中，刺激在一个方面是恒定的，但是作为距离其他维度上一个特定点的线性函数而变化着，例如，一个分级圆盘，从中心到边缘一致地变得更淡或更浓。正如马赫（Mach）于1865年发现的那样，这些分布看上去一致，我们还必须补充一点，这些分布发生的区域，在我们的视野中产生一个充分界定的单位。实际上，两个特例必须加以区别；在第一特例中，一致性是完整的，而且在该特例中，所见的区域性质是一样的，好像刺激的平均数一致地分布在该区域上面一样。在第二个特例中，一致性并不完整，而是仅仅涉及颜色的一个方面（它的色质），而不是涉及其他方面（它的“明度”或“亮度”）。一个大房间里的白墙看上去遍体雪白，但是，在它远离光源的地方，白墙就变得“暗一点”，“亮度差一点”。让我们把第二种特例的讨论推迟到后一章中，现在我们回到第一种特例上来。

    如果我们通过引入精细轮廓的方法把一致地变化着的刺激区域分成两个或两个以上的区域，那末，色彩的一致性便将在整个区域内消失，而且只保留在新形成的部分区域内，这些新形成的部分区域现在看来彼此不同，每一个部分区域均按其自身的平均刺激而不同（考夫卡，1923年a）。当刺激的变化不一致时，也可能发生同样情况；在该情况中，变化率（rate of change）逐点发生变化。在第一种情形里，i＝f（x），其中i代表刺激强度（或者其他充分界定的特征），X代表与任意来源（arbitary origin）的距离，因此出di／dx=常数，可是，在第二种情形里，不仅i＝g（x），而且出di／dX＝ψ（x）。如果二阶导数d²i／d²x的绝对值不是太大的话，那么，该区域看上去仍将一致。在这些条件下，刺激的平均数仍将有效，正如我已经证明过的那样。

    但是，如果变化率的变化过大的话，便会产生某些新的东西，这就是我打算讨论的第二种情况。为了更好地理解这种情况，我们将使用刺激分布的图解，这是我们在本章开头时已经介绍过的（见边码p．111）。一致的变化用一根向着X轴倾斜的直线来表示，如图48a所示，而第二种类型的分布则由图48的b和C来例证。如果我们选择一个P点，那么，当刺激的变化处于恒定状态时（图48a），它的刺激将与其毗邻的平均刺激一样。但是，当变化率随着X而变化时，这种情况便不再正确了。于是，在图48b里面，P点将比它周围的平均刺激接受更多的刺激，而在图48c里面，P点将比它周围的平均刺激接受更少的刺激。在这些条件下，如果P点的刺激和它毗邻的平均刺激之间的差异十分大的话，那么将会出现一种奇异的和有意义的结果，马赫早在70年以前就已经发现了这种结果。当P点的刺激比它毗邻的平均刺激更强时，P点处将出现一根明线，可是，当P点的刺激比它毗邻的刺激更弱时，P点处将出现一根暗线，尽管在这两种情形里，一侧的刺激比P点刺激更弱，而另一侧的刺激比P点刺激更强。当这些刺激是由转动的圆盘提供时，那么这些线便自然而然地变成了圆环。于是，马赫环（Mach rings）证明，部位结果不是部位刺激的结果，而是有赖于刺激在大范围里面的分布，这一点已由马赫本人十分清楚地指出了（1865年，1885年）。我们只想在一个方面对马赫的理论作进一步阐述。马赫认为，这种结果纯粹是色觉，而且他的实验作为与赫尔姆霍兹（Helmholtz）的心理学理论相对立的生理对比理论（physiologi－cal theory of contrast）的最后一个证明，出现在许多早期的教科书中，可是现代的教科书则倾向于把它省略了。但是，圆环的出现（也就是说，一个区域内的新形状）是一个组织问题。这个问题是由M．R．哈罗尔（M．R．Harrower）和我本人根据这一观点提出的，而且，我们明确地阐述了这样的事实，即有利于特定形状组织的一些条件将会产生马赫环，而当一般情况不太有利于这种组织时，这些圆环将不会出现或者不太明显。我们已从利布曼（Liebmann）效应中了解到，亮度差异在产生分离方面要比仅仅产生色彩差异来得更加有力。因此，哈罗尔博士和我得出结论认为，如果马赫环是组织结果的话，那么单单色彩变化是不会产生马赫环的。索利斯（Thouless）已经开展了这样的实验，这些实验证实了上述的结论；在一组精心设计的实验中，我们证实了索利斯的发现，与此同时，确立了针对马赫环而设立的硬色和软色之间差别的效验。

组织和简洁律：最小和最大的单一性

    现在，我们已经到达了我们讲座中的某个阶段。我们已经在若干不同的条件下对组织进行了研究，而有关这种组织的一些有效原则也已经建立起来。把我们的成就与本章的引言相比较是适当的，在该引言中我们系统阐述了我们研究的指导原则，也即简洁律（law of pragnanz），它把产生的静态组织（stationary or-ganizations）与某些最大最小原理（maxim－minimum principles）联系起来了。实际上，该定律遍布于我们的整个讨论；我们已用各种形式遇见过这个定律，如统一（unity）、一致（uniformity）、良好的连续（good continuation）、简单的形状（simple shape）和闭合（closur）。但是，还遗留一点，它在开始时曾被提及过，但在后来的讨论中没有展开，那就是我们所谓最大事件和最小事件的单一性之间的差别。现在，我们必须根据这一观点来进行我们的讨论，并补充一些证据，以便为我们的区分提供更多的材料。

    概略地说，最小限度的单一性将是一致的单一性，而最大限度的单一性则是理想的清晰度的单一性。在我们的例子中，两者均用图形表示；第一种在后象（after-image）实验中用图形表示，并在减弱组织的外力的其他效应中用图形表示；第二种则体现在良好的形状和良好的连续等例证中。我们能否从产生这两种结果的任何一种原因或条件中得到一点暗示呢？遗憾的是，我们对我们的问题缺乏特殊的系统调查，但是，如果我们用其他一些事实来加以补充的话，则我们可以从我们熟悉的一些事实中得出某些结论。例如，当我们注视一幅肖像照片时，我们看到一张具有形状和表情的脸；但是，如果我们试着发展这幅肖像的后象，那么，我们所见的一切便是一团模糊不清的东西了。后象缺乏清晰性，这是与知觉相比较而言的，但是却比知觉一致得多，前者表现出最小程度的简化，而后者则表现出最大程度的简化。

    然而，要想产生一张脸的后象是不可能的，原始的脸一定比任何一张普通的照片具有更强的对比度；于是，图49将产生关于冯·兴登堡总统（President Van Hindenbury）的一个很好的后象。

    其次，让我们看图50的图形。倘若你偶然一瞥，你会看到这幅图形好似乱七八糟的些线条。但是，当你被告知，这幅图形是一张实际的图片，并要求你努力去发现它时，你便会发现，这是一个胖乎乎的老年绅士的幽默脸庞。

    关于我的上述那个例子，我想回到调节（ac- commodation）的讨论上来（见边码 PP． 119f），在这一讨论中，我们学会了把调节的功能作为一种为清晰度服务的运动反应未理解。现在，让我们想像一下，当你十分疲劳但又不得不出席晚间演讲时，对这样的讲座你会比平时更感厌烦。这时，会发生什么情况呢？你会将目光集中于演讲者，藉以保持清醒，但你却不会注意他的形态，正像福斯特博士（Dr．Faust）书房中的那条卷毛狗一样，那位演讲者的形象将逐渐增大，最后或多或少与房间的墙壁融合在一起。显然，你的调节已经让步，现在你的调节以这样一种方式运作，它给你最小的清晰度，同时却给你最大的一致性。

    这些例子暗示着下述一种结论：当有机体处于积极状态时，用亨利·黑德爵士（Sir Henry Head）的术语来讲，当有机体处于高度警戒状态时，它将产生良好的清晰度；当有机体处于消极状态时，也就是警戒程度低下时，它将产生一致性。在第三章结束时（见边码p．102）提出的警戒解释中，我们曾提出，高度的警戒性意味着有机体具有可以任意调遣的许多能量。如果我们将这一解释用于我们上述的例子，那么，它意味着最大程度的单一性（也就是高度的清晰度）会在有机体可供调遣的能量巨大时发生，而最小程度的单一性（也就是一致性）会在有机体可供调遣的能量微小时发生。我们的所有三个例子均适合于这种解释。疲劳或低的警戒性是能量下降的条件。在第二个例子中，寻找有意义的图形的态度产生了清晰度，这显然也是较大的可供调遣的能量的例子，因为在这里具有能量储存的自我系统（Ego－system）承担了构造。第一个例子是最难理解的。但是，一张普通肖像的负效应和兴登堡图形的正效应之间的比较扫除了这一困难。在第二个例子中，外部的组织之力要比第一个例子中强大得多，这是由于在不同的场部分之间刺激的更大跳跃之故，而更大的清晰度就是由于这种更大的组织之力。因此，如果较大的清晰度意味着在该过程中消耗了更多能量的话，那么，这些较大的力一定也释放了更多的能量，正像一台正在运作的电动机要比一台闲置的电动机消耗更多的能量一样。

    我已经强调了能量和清晰度之间的这种联系（也许我所提供的证据相当不充分），这是因为，从理论上讲，这种联系是坚实的。让我们重复一下苛勒的一段话：“最后的不依赖于时间的分布包含了能够作功的最低限度的能量”（见边码，p．108）。这种情况尽管在一切情形里都是正确的，但在特定的情形里需要一个十分重要的系定理（corollary）。假定我们正在考虑的系统变化由一个相对来说小的亚系统（subsystem）和一个大的蓄积库组成（从这个蓄积库中我们可以根据需要提取尽可能多的能量）。在我们将我们的观点用于这一情形时，我们必须把最后的能量变得最小的那个系统当作由亚系统和蓄积库组成的整个系统。我们发现，在这一过程中，小的亚系统从蓄积库中尽可能多地提取能量，以致于在这一过程之后，它自身的能量比它先前的能量更大。苛勒在1924年将这一原理用于有机体的成长及其不断增加的清晰度。看来，这也同样适用于我们目前的问题：如果特定的反应系统能够吸取许多能量的话，那么它就会这样做，从而获得清晰度，也就是说，获得最大程度的单一性；如果它的能量供应中断，或者仅仅局限于很小的范围之内，那么将产生最低程度的单一性。

来自数量顺序和意义等观点的组织

    到目前为止尚未忘记本书纲要的读者（本书纲要在第一章中已经刊布），可能会怀疑作者在本章的详细讨论中是否已经忘记了他的一般观点。因此，让我们暂停此处，看一看我们迄今为止对于在本书开头时提出的问题作出了什么贡献，如果确有什么贡献的话。我们看到了心理学在其整合作用（integrative func－tion）中的特定价值，我们的科学正处在自然、生命和心理的交会点上。我们的讨论有没有对这种整合作出过贡献呢？我们已经从这三个会聚领域的科学中提取了三个指导性概念，它们是数量（quantity）、顺序（order）和意义（meaning）的概念。根据这三个术语，我们的讨论意味着什么？

    数量

    我认为，就数量而言，我们的讨论已经证明了这样一些推论，这些推论是当我们第一次研究量和质的关系时达到的。我们的简洁律具有量化的特征，该特征同时也是质的特征。作为最大和最小的原理，简洁律是定量的，而作为单一性原理，它又是定性的。显然，量和质的特征并非两个彼此独立的特征，而是同一原理的两个方面。在实际的实验中，质的方面领先；对于任何一种实际的组织来说，我们未能提供确切的量化公式。但是，作为实际的组织，单位和形状必须具有一个公式，该公式从数量上对单位和形状加以表述，正如物理格式塔也有它们的公式一样。我们的质的知识与这种量的知识只是在精确性程度上有所不同，而不是在种类上有所不同。

    顺序

    我们发现，有效的组织定律解释了我们的行为环境为什么是有序的，尽管刺激的空间复杂性和时间复杂性有点令人手足无措。单位正在形成，并保持着与其他单位的分离和相对的隔绝状态。请考虑一下，当你的双眼连续不断地东张西望时，视网膜的组成要素将会发生什么情况：如果双眼以迅速的相继方式注视物体，而且没有任何顺序，那么，视网膜的要素将时而受到白光的刺激，时而又受到绿光的刺激；一忽儿刺缴变强，一忽儿又变得很弱；伴随着绿色的是红色或蓝色，一种万花筒般的变化。与视网膜各点上刺激的忙碌景象相一致的是什么东西呢？一个完全稳定和井然有序的世界；当我的眼光扫视时，我的书桌上的香烟盒仍然是香烟盒，台历仍然是台历；我在我的行为环境中体验不到变化，尽管我在“我自身”内部体验到一种变化，感觉到我的双眼在静态的物体上移动。确实，我们对这种特殊的效应尚未作出过解释，但是，我们看到，如果没有我们的组织原则，物体便不成其为物体，因此，由这些刺激变化产生的现象变化将如同刺激本身的变化一样无序。于是，我们把顺序作为实际的特征而接受下来，可是，找们无需特殊的动因（agent）去产生顺序，因为顺序是组织的结果，而组织则是自然之力的结果。以此方式，我们的讨论表明了自然如何产生顺序。

    意义

    最后，我们的讨论为我们提供了一个理解“意义”（significance）的基础。良好的连续和良好的形状是有力的组织因素，而且，两者在实际的意义上都是“可以理解的”：一根线在其自身内部携带着自己的定律，一个有形的区域或容积也一样。由于外力的作用而违反这个定律被视作是一种违反；它们与我们的合适感（feeling of the fit）发生冲突，从而有损于我们的美感。我们在任何时刻看到的形状并没有通过将部位价值分配给每一个形状的空间要素而被恰当地描述，而是被视作一致的整体；它们像威特海默的天堂访问者听到天堂的音乐一样，而不像台子或音调的纯经验公式那样（这是威特海默的其他一些天堂探险家能够详加阐述的）。

    我们的讨论处理了一些十分基本的物体，这些物体远离心理的各种表现形式，在这些表现形式中，“理解的”心理学家对它们发生兴趣。但是，即便是这些微不足道的物体，也揭示了我们的现实不只是基本事实的并置（collocation），而是由一些单位所组成，在这些单位中，没有一个部分是靠它自身而存在的，其中，每个部分都指向它自身以外的地方，从而意味着一个较大的整体。事实和意义不再是属于不同领域的两个概念，因为在内在地一致的整体之中，一个事实始终是一个事实。如果我们把问题的每一点分离出来，逐一予以解决，我们便无法解决任何问题。由此可见，我们确实看到了意义的问题如何与整体及其部分之间的关系问题如此紧密地相联结。我们曾经说过：整体大于它的部分之和。我们还可以更加确切地说，整体除了它的部分之和外，还有其他某种东西，因此，计算总和是一种毫无意义的方法，而部分-整体的关系却是有意义的。