|
在产业中，严格的纯粹竞争或垄断的条件即使存在，也是很少见的。就连常常为人引为竞争性厂商典型例证的农场主也保留存货。而且，同一种商品在不同地区的价格差距有时也高于运输成本。另一方面，即使一种产品或服务只有一个卖者，它也必然面临替代品的竞争。因此，垄断和竞争的纯粹形式最好被看成在一个系列中的两端。
例如，我们可以把垄断竞争（下章将讨论）归为一个有着许多竞争模型特征的模型、在这个系列的另一端，我们又发现可以归入寡头垄断范畴的模型，这主要由在一个产业中的厂商数来区分。尽管当前尚无寡头垄断理论，各寡头垄断模型都强调彼此依赖这一基本概念。寡头垄断这一术语意指在某产业中存在不止一个厂商；人们一般认为这一数量范围在二个到十二个或更多的厂商之间。此外，寡头垄断模型是有区别的。一些模型具有较多的接近竞争的市场特征，而另一些只有少数厂商的模型则有许多类似分享垄断的特征。
古诺模型
各种寡头垄断理论之间的主要区别之一在于对厂商间互相依赖关系性质的描述。一家厂商对另一家厂商作出反应的方式被称为“反应函数”。我们首先论述的古诺理论就含有一个非常简单的反应函数。
一个多世纪以前，安托瓦纳·奥古斯丹·古诺（AntoineAugustin
Gournot）创立了双头垄断理论。不幸的是，古诺这一理论直到本世纪30年代才传播开来并受到广泛的讨论。古诺的模型本身是饶有兴味的，并常常被当作进一步分析的基础。
古诺模型的假设
古诺基本模型的假设如下：
1．产品是同质的。
2．有两个买者，以后将推广为几个卖者。
3．每个卖者都有相同的边际成本。
4．每个卖者对市场需求曲线上的短一点都有完备的信息。
5．市场变化是指产量变化而不是价格变化。
6．最后，古诺的关键假设涉及的行为法则是：两个垄断者之一在选择他的或她的产出率时，假定对方的产出将保持不变。
关于竞争对手反应函数的最后这一假定，使古诺的理论成为讨论竞争对手反应的其他多种寡头垄断理论所追随和模仿的经典理论。毕竟，竞争对手的行为是寡头垄断的基础；它为完全竞争和纯粹垄断理论所忽视。古典理论简单地假设了几种被认为理所当然的有意识的竞争行为，而这又常常是以对竞争者行为的假定为基础的。可将其与现代假定有一个总利润最大化的目标，并预言每个有意识地达到这一特定目标的经济主体行为的类型及成功与否的理论比较一下。古诺模型假定的行为方式是掩耳盗铃式的，即两个双头垄断者之一活动时仿佛他或她的行动不会诱发对手的产量反应。这基本上是一种厂商不根据经验调整自己行为的模型。按照这一假定，在任何情况下，古诺都能表明两个寡头垄断者可以接近均衡的产量和价格。
古诺的均衡理论
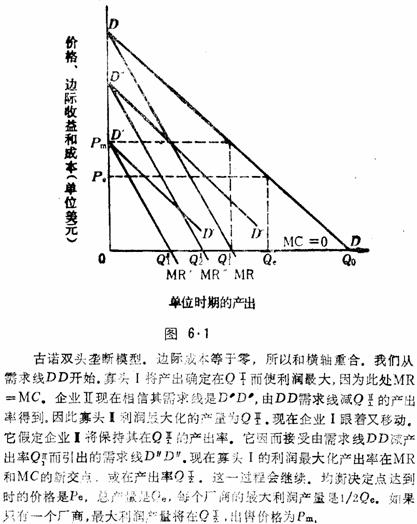
为了理解模型的功能，我们从某商品的行业需求曲线开始讨论。为保持古诺原文的风貌（他用自流井作为这一商品），我们将用矿泉水为该商品。为了简化起见，我们假定需求曲线是线性的，边际成本等于零。
请看图6．1。行业需求线是DD，边际收益线为MR。两个企业是Ⅰ和Ⅱ。企业开始移动，企业Ⅱ暂时不动。因此，DD是企业Ⅰ面临的需求线；它确定的产出率在边际收益等于边际成本处。它是边际收益线和水平轴相交处的产量。它的产出率为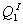
。这里上标指厂商，下标指时期或“阶段”。因而，
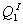指寡头Ⅰ在第一阶段或第一期生产的产量。这是在假定另一个寡头将保持其产出为零的条件下得出的。
现在厂商Ⅱ进入市场。它把厂商Ⅰ的产量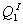视为既定。厂商Ⅱ相信其需求线是DD减
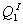的产出量。它的需求线是由DD减去厂商Ⅰ的产出率Q11而得到的D’D’。厂商Ⅱ将通过使产量确定在新的边际收益线MR’和代表其边际成本线的横轴的交点而使利润最大。厂商Ⅱ将生产
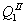。厂商Ⅰ接着又移动。它假定厂商Ⅱ保持其
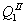的产出率。厂商Ⅰ设想，其新的需求线为市场需求线减厂商Ⅱ的产出率。这一新的需求线是图6.1中的D”D”。这条需求线派生的边际收益线记为MR”。厂商Ⅰ会改变其产出率，以使边际收益MR”＝边际成本＝0。这一点位于MR”和水平轴的交点处，或者在产出率QE处。
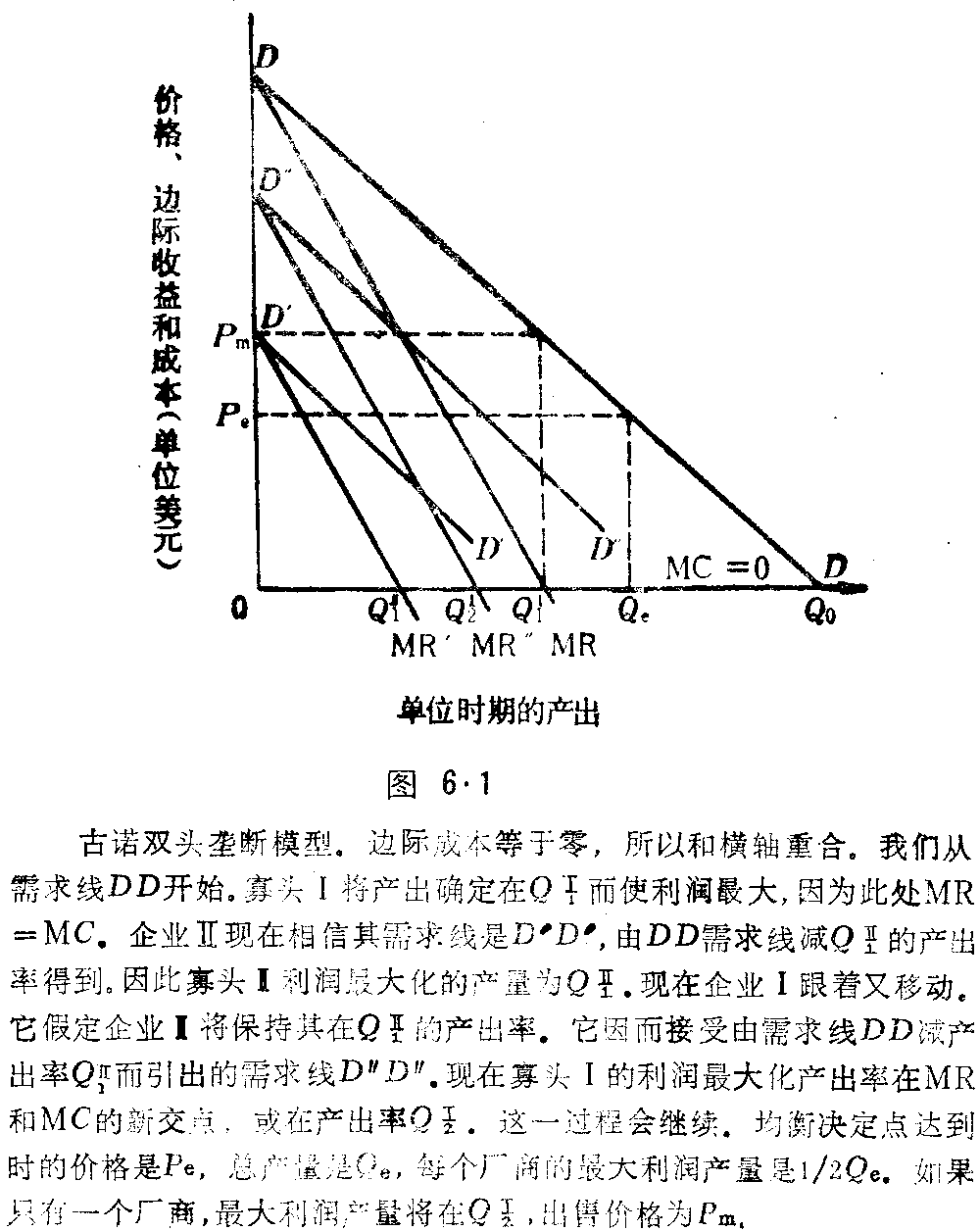
每个厂商都把另一个厂商的产量视为既定，然后通过选择适度的利润最大化产出率使其利润达到最大。这一新产出促使竞争者的需求线接着发生变化，竞争者便选定一个新的较低价格。然而，这一过程不会无限持续下去。最终，如同图6．1中两个厂商的情况那样，每个企业的产出率将趋近于1／3Qo的均衡量。每个厂商出售其产品的价格是Pc。注意这同完全竞争的结果不同，完全竞争要求价格等于边际成本，而此处边际成本为零。因此在古诺双头垄断模型里，价格高于边际成本，产出率少于完全竞争条件下的产出率。但是，在古诺的模型中，产出量要比在纯粹垄断条件下的产出量大。在纯粹垄断中，产出率将为QII。因为在此MR＝MC。在图6．1中的垄断价格将为Pm。
反应函数
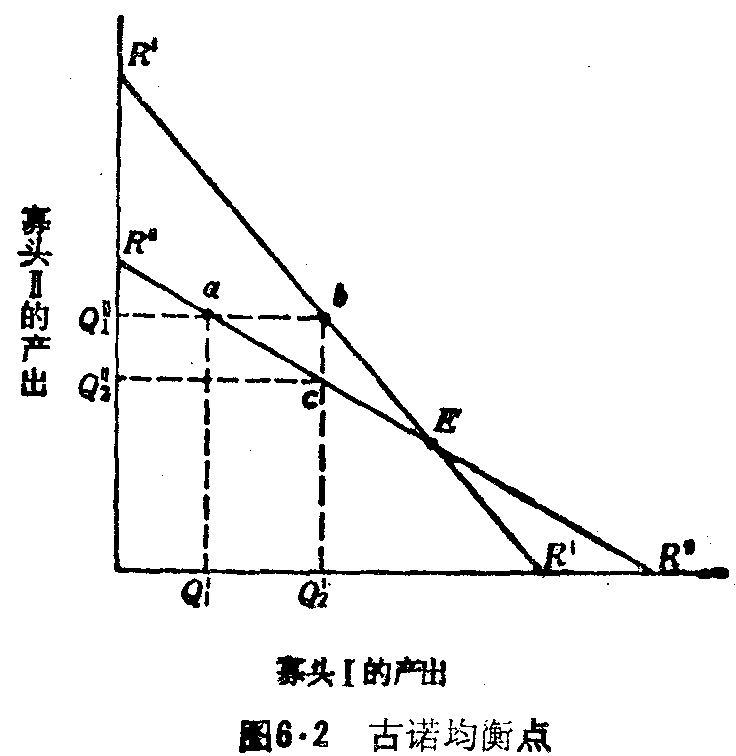
对寡头Ⅱ提供的任何产出水平，都存在寡头Ⅱ使厂商Ⅰ的利润最大的产出。在图6．2中，这一系列产出点构成寡头Ⅰ的产出反应曲线RⅠRⅠ。同样，在图6．2中，寡头Ⅰ的产出反应曲线假定为RⅡRⅡ。
如果寡头Ⅰ生产产出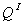 ，寡头Ⅱ将在其产出反应线上移动到与a，生产
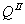。当寡头Ⅱ的产出
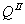为其最大产出时，寡头Ⅰ现在想把产出增加到
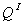（点b）。在厂商Ⅰ的扩展给定后，寡头Ⅱ将力求生产较低产量
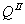（点c）。这一过程将继续下去，直到两个寡头达到产出E，此点为均衡点。这一均衡点常被称为古诺均衡点。
伯特兰模型
古诺双头垄断分析的一个变种是由约瑟夫·伯特兰（Jo－seph Betrand）提出的，分析被证明是对古诺理论的混乱的、也许是错误的批评。伯特兰的双头垄断模型和古诺的模型相似。区别在于，伯特兰假定对手调整的是价格而不是产量。在伯特兰式的调整过程中，假定另一对手将维持他或她的现有价格，则每个竞争者将少量降低他或她的价格以占据整个市场。生产者被假定是同质的，所以开价较低的卖者便占据了整个市场。不过，每当一个卖者降低价格时，另一个卖者当然也会降低其价格，直到足以占领整个市场为止。这一降价过程继续下去，直到价格降低到边际成本或竞争性价格为止。所以，尽管我们只是将调整变量由产量改为价格，但伯特兰模型解出的却是竞争性市场的结果，而古诺解则不是。在任何时期供应给定产量的古诺式双寡头之一必定在限制他或她可以取得的市场份额，而伯特兰式垄断者报出的价格使他或她可以占据整个市场，因为所有消费者都将转向价格较低的卖者。
当我们认识到一旦在市场上不止有一个厂商，因而要达到总利润最大化就需要某种形式的合谋时，伯特兰的结论也许看来就不那么奇怪了。在伯特兰的模型中不存在合谋。
假定不同，厂商相信其竞争者对自己的活动作出的反应也就不同。这是很重要的，伯特兰模型和古诺模型就说明了这一点。这两个模型假设不同，也就意味着双头垄断者对其面对的需求条件理解不同，这导致截然不同的结果。
埃奇沃思模型
埃奇沃思模型对古诺的假定作了两点修改。第一点是，两个矿泉水生产者的生产能力都是有限的。在价格为零处的需求量超过单个厂商的供给能力。第二点修改是，在极短的时期里，矿泉水市场上会出现两种不同价格。
最重要的是，埃奇沃思不仅假定每个寡头选择使利润最大的价格，而且也假定选定这一价格时，另一个寡头不会改变其价格。
在埃奇沃思模型中的趋向均衡的过程
埃奇沃思模型指出，在长期中，双寡头的产品将有同样的价格，他们将等量瓜分市场。因此，我们在图6．3中表明寡头Ⅰ的产出率位于右面，寡头Ⅱ的产出率位于左面。共有的纵轴表示单位价格。寡头Ⅰ的需求线是dⅠ，寡头Ⅱ面临的需求线是dⅡ，两条需求线都假定，在长期中，两个卖者的价格相同。两条对称的需求线的每一条，等于市场需求的二分之一。
寡头Ⅰ和Ⅱ的最大生产能力分别为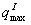
和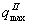
。像在古诺模型中一样，卖者不断追求最大利润，并不能根据经验作出调整。埃奇沃思模型也是一个非边干边学模型。
我们从寡头Ⅰ（暂时是唯一的垄断者）开始，他的利润最大化价格是P1。之所以此处使利润最大化，是因为与之相应的产出率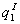
位于边际收益线和水平轴的交点，在这里，水平轴也是边际成本曲线。为简化起见，我们没有画出边际收益线。（检查一下该图的精确性，看看
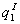是否位于O点和需求线与水平轴相交点之间的正中。
然而，寡头Ⅱ看见寡头Ⅰ的价格P1后，认为将他或她的价格定在P1以下，就可以把消费者从继续维持P1的寡头Ⅰ那儿引开。
然而，这一价格定下以后，寡头Ⅰ发现，如果价格定得更低的话，消费者就会离开寡头Ⅱ。这场价格战会继续到价格Pn。在这一价格，两个厂商都无法再增加产出；因为这时的产出等于其生产能力。在价格Pn，寡头Ⅰ和寡头Ⅱ是在按他们各目的最大产数量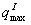
和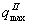
生产。现在将发生什么情况？很明显，如果P1是使利润最大价格，那么，一个寡头会发现，若拟价格提高到Pn之上，他或她就能增加总利润。另一个寡头会紧紧追上，价格又会上升。团此，埃奇沃思模型没有一个最终解。它仅仅提出了价格和在双寡头市场的产出率变动的限度。出现的最高价格将为P1，最低价格是Pn。不存在唯一的均衡价格；也不存在唯一的均衡产量。但是有一个一定范围的可能价格和产出。
在继续探讨其他寡头垄断模型之前，我们在此应注意，提出古诺和埃奇沃思模型不是因为它们恰如其份或符合现实。我们介绍它们是为了演示将寡头垄断理论化的困难。当寡头间彼此依赖时为取得厂商所面临的需求线而碰到的困难问题，是寡头垄断理论中所有总是的关键。
霍特林模型
埃奇沃思模型的说明描述了只有两个卖者的市场中的不稳定因素。霍特林（Hotelling）在1929年对这一观点提出挑战；他认为价格或产出的不稳定并非是寡头垄断的基本特征。
假设
霍特林使用的假定如下：
1．同质的产品由两个在地理位置上分开的厂商出售。
2．两个卖者史密斯和琼斯位于图6．4表示的某一线性市场段上。这个市场共有四部分——每个卖者的两边各有一部分——每个消费者必须支付他或她自己的运输成本，假定每单位距离的运输成本为C。
3．买者均匀地分布在市场上，每个买者单位时间的购买量给定，需求完全无弹性。
内容
在上述假定下，霍特林的双寡头可以相机选定价格。然而，琼斯的价格不能多于史密斯的价格加由史密斯的营业地到琼斯营业地（x＋y）的运输成本。换言之，琼斯的价格Pj不能超过史密斯的价格Ps加C（x＋y）。我们由此得知，琼斯一直在图6．4中标为J的市场上服务，而史密斯一直在市场S处服务。琼斯和史密斯两处之间的地区将由他们两人服务；琼斯服务于X区，史密斯将服务于Y区。X和Y的实际距离取决于价格Pj和Pr。在分界点，同质商品的销售价格在此点对琼斯和史密斯来说是相等的，因此买者对两位卖者是无动于衷的。换言之，在分界点，琼斯的价格加运输成本一定等于史密斯的价格加运输成本，或Pj＋CX＝Ps＋CY。
霍特林再增加等式：
市场长度＝J＋X＋Y＋S
现在他就能表明这两个等式决定均衡价格和均衡产量了。
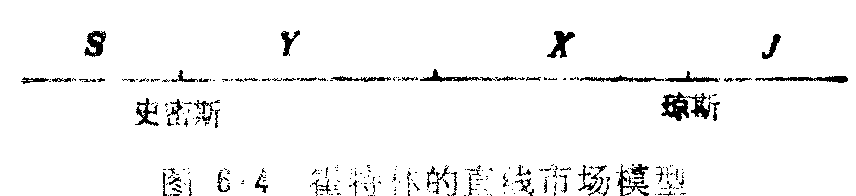
霍特林对埃奇沃思和伯特兰的批评
霍特林模型显然是对埃奇沃思和伯特兰的批评。霍特林不同意消费者由一个卖者突然转向另一个卖者是市场的特征这一观点。他预期价格的下降实际上吸引不了多少消费者。因而他认为，只要消费者逐渐转向竞争者，市场就仍将保持稳定。对双头垄断模型的批评
我们已经指出，古诺和伯特兰的模型意指双寡头每一方都存在自我幻觉。这种自我幻觉给许多研究者——包括赫维茨（Hurwicz）——带来了麻烦。
当一个人的理性活动依赖于另一个人的可能发生的行为时，就无法完全解决定义这部分个人的“理性经济行为”问题……［当讨论寡头垄断时］个人的“理性行为”决定于“其他人”的行为方式是否能假定为预先可知。
但是，如果“其他人”也根据理性行事，那么“其他人”的行为是无法预知的！因此，逻辑的死胡同出现了。
例如，在古诺模型中，每个卖者都对他或她的对手的行为作了假定。每个双寡头都知道，除了在均衡中之外目前的情况是与将来截然不同的。而且，如果双寡头不能确切地了解未来，他或她就无法改善处境。
进入与分解
古诺模型预期，当更多的企业进入市场时，总产出会增大，市场将趋向价格－产量的竞争解。但是，如果我们要接受古诺模型，我们就必须分辨由于新企业进入而导致的厂商数增加和现有企业的分解而导致的广商数增加。古诺实际上未提进入的这两种类型；他简单地给出厂商数而没有解释它们的类型。但是，如果我们看一下他假定的成本函数，那么双寡头、三寡头甚或寡头垄断都无法持久，因为成本没有随着企业的规模或数量而变化，而任何高于长期边际成本的价格都将吸引进入。除非存在进入的制度限制或基本资源归现有企业所有（像古诺选用的自流井事例），否则持久的寡头垄断无法存在。
没有合谋的可能性
古诺和伯特兰的模型都忽视了合谋的可能性。如果合谋产生，总会增加总利润。如我们下面会看到的一样，合谋通常会增加净福利，但不幸的是对合谋者来说，总存在着某种使每一个企业欺骗的诱因。这种活动趋向导致任何已签定的勾结协议的失效。
对批评的反驳
上述的简单双寡头模型主要在假定的非现实性方面受到批评，然而，对于“现实的”假定是否合适，肯定会有一场方法论的争论。从与第14－21页上提到的相同的非常严格的科学方法论观点看，方法的预见力，或起码是解释力，而不是其假定的现实性，是检验理论有效性的标准。因此，要回答的问题是，“在现实世界里卖者的行为是否符合古诺或伯特兰的决策规则？”当然，这是一个经验的问题。一些研究者已经发现了支持这种理论的偶然的例证，然而，尽管几乎没有做过经验检验，高乐波和罗伯茨（Gollop
＆Roberts）却毫不含糊地否定了古诺的双寡头理论。他们运用焙咖啡业对数生产函数未能拒绝行为相互依赖的假定。
众多的模型
我们现在转而探讨包括两个以上厂商的寡头垄断模型。我们将从考察一个简单的模型开始，进而看一下由施蒂格勒、斯威齐、张伯仑、费尔纳、纳特和穆尔以及其他人提出的模型。
一个简单的寡头垄断模型
假定 为了在最一般的水平上开始讨论寡头垄断，我们做出5点假定：
1．与行业需求线有关的LAC曲线的形状和位置决定了该行业只能容纳少量的有效率工厂和厂商。
2．厂商（和工厂）的LAC在一定产出范围以外是往上倾斜的（没有自然垄断）。在边际成本总是正的和在LAC之上时，每个厂商的总成本曲线是连续的和正常的。
3．由于厂商水平工厂数量较大的不经济、皮托拉斯活动的可能性等等，厂商只能有单个工厂。换言之，在共同所有和控制下的工厂联合成本太高了，以至联合不可能存在。
4. 不存在进入或退出该产业的壁垒；进入退出是自由的。
5．厂商生产同质的（相似的）产品。
垄断寡头的需求线
现在我们面临画出一个垄断寡头的需求线的困难任务。因为这个垄断寡头不是唯一的垄断者，所以我们不能使用该产业的需求线。我们也不能使用在市场出清价格上的水平需求线，因为垄断寡头并不是一个完全竞争者。在我们对垄断寡头之间的相互作用做出某种假定前，我们无法给出垄断寡头的需求线。我们必须对我们将要讨论的反应函数有所了解。每个垄断寡头都相信其他寡头不会对其价格和（或）产量变化作出反应吗？如果典型的垄断寡头相信其他寡头会作出反应，那么我们必须详细说明寡头预计其他寡头将以什么方式作出反应的。在完全竞争模型中，因为每个企业都能按现行市场价格卖掉所有它想卖掉的商品，所以每个企业都无视了其他企业的反应。在纯粹垄断模型中，垄断者不必担心对手的反应，因为根据定义不存在竞争对手。这种互相依赖关系是每一个寡头垄断模型的核心，可以想象，每作出一个关于垄断寡头之间的相互作用的新的假设，也就产生一个新的寡头垄断模型。对这种最简单的寡头垄断模型，我们假定如下：
每个厂商都预期和确知，价格的任何变化都将引起该产业所有其他厂商的攀比。
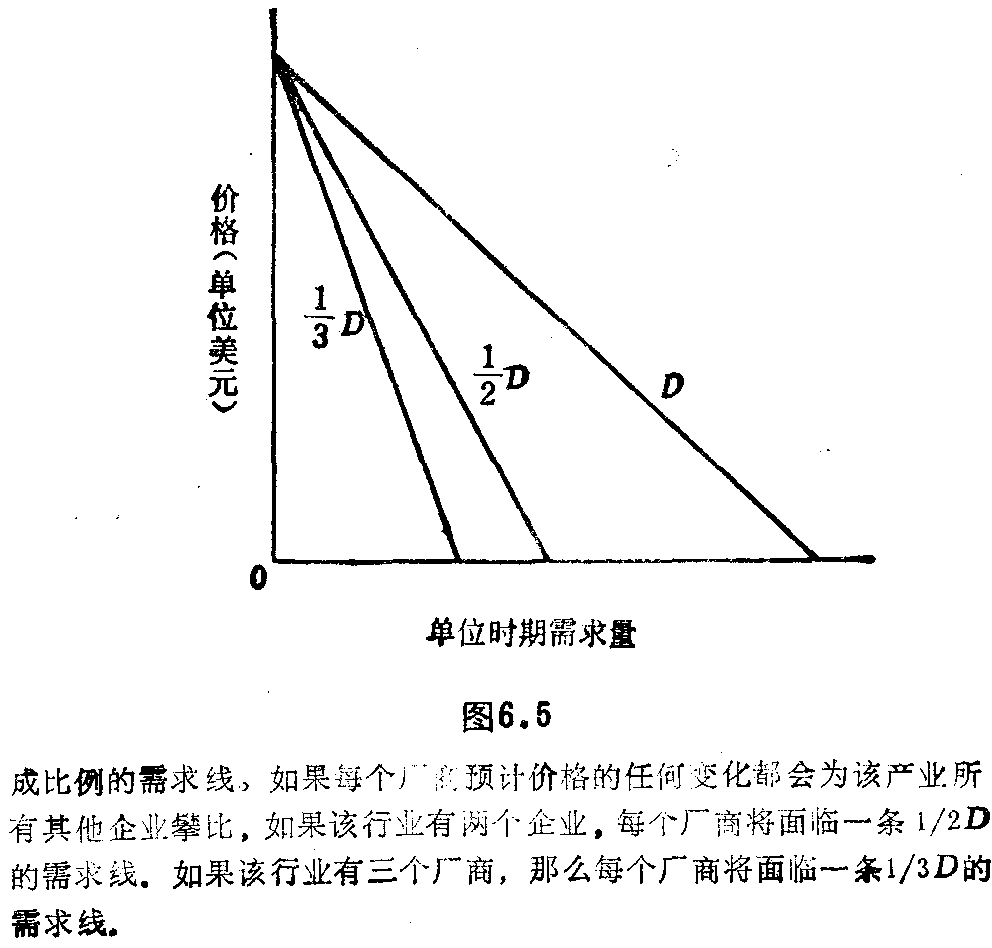
在图6．5中，我们可以见到这一假设的结果。这个行业的需求线是D。如果该行业仅有两家厂商，那么这两家厂商都相信其需求线等于标明1／2D的那一条。这里根据的是我们的假定，即该行业无论选定什么价格，都将引起竞争对手们之间的攀比。如果我们设该产业有3家厂商，那么每个垄断寡头所面对的个别需求线将是1／3D。
均衡的厂商数
因为我们已经假定不限制出入，并假定所有厂商的成本曲线相同，所以我们可以通过考察长期平均成本曲线来确定将留在该行业的厂商数。这条曲线如图6．6所示。如果该产业有一个厂商，其他厂商就会被吸引过来，因为在较大的产出范围内，长期成本曲线应于产业需求线D的下方。如果该产业有两个厂商，那么仍然存在进入的刺激。最后，如果该产业有三个厂商，第四个厂商就不愿意进入，因为LAC曲线总是在成比例需求线1／4D的上方。根据我们的假定，如果该产业有四个厂商，那么没人能够位于长期平均成本之上。他们都将蒙受经济亏损。
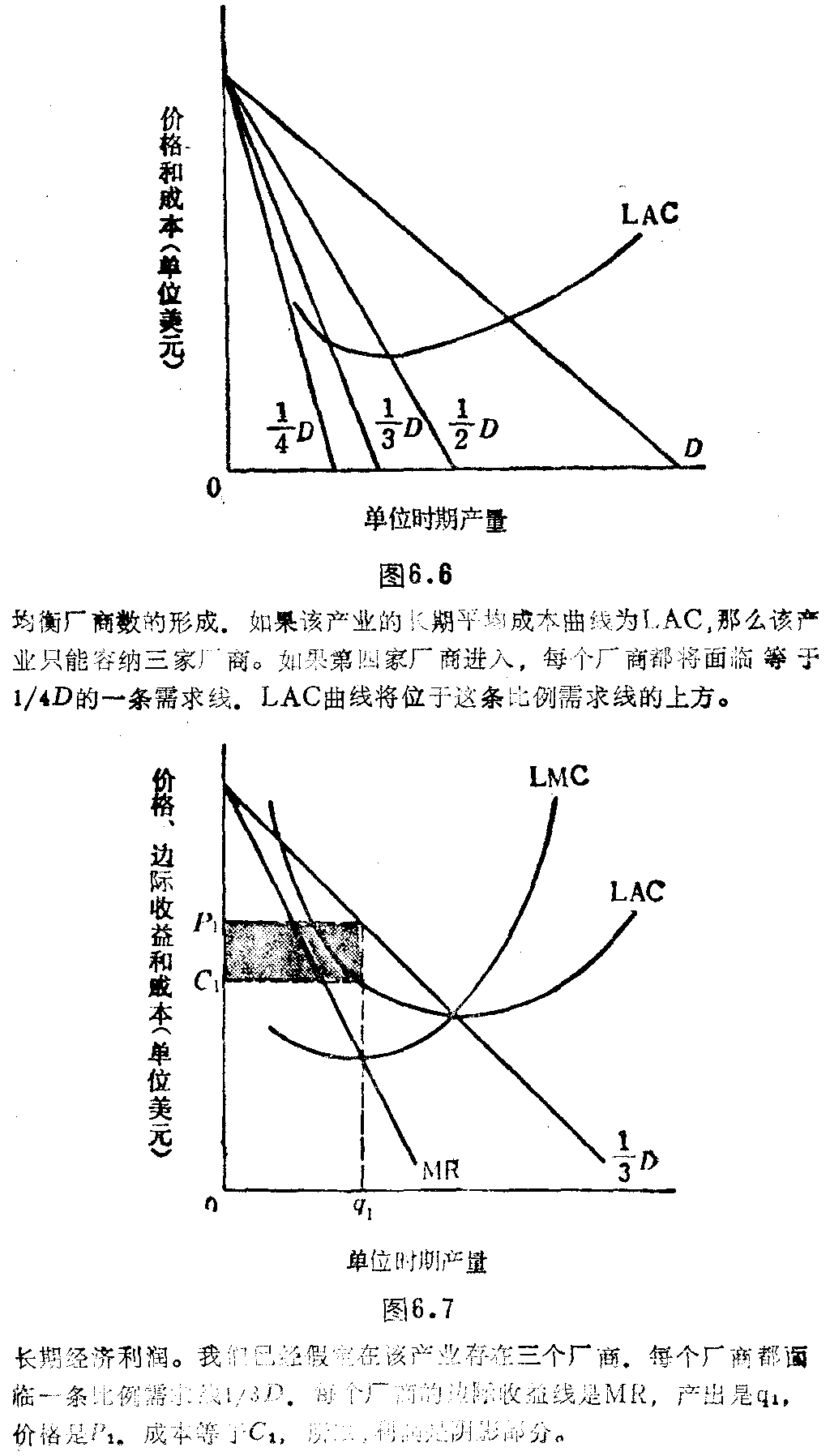
在这个简单模型中，从长期来看，获得经济利润是可能的。在有三家企业时，通过移动每个垄断寡头的比例需求线可以发现这一点（图6．7）。三家厂商中任何一家面临的需求线都是1／3D。长期平均成本曲线假定为LAC，长期边际成本曲线是LMC。每个垄断寡头的使利润最大的产出率在边际收益和长期边际成本的交点，或在产出率q1。每个厂商的产品销售价格统一为P1。单位成本在LAC给定的情况下是C1。单位时间的经济利润等于图6.7的阴影部分。
在这个模型的给定假设下，这就是长期的均衡。
互相依赖和不确定
让我们改变我们的假定。厂商现在意识到他们是彼此依赖的，然而他们仍然不能完全确定他们是如何依赖的。换言之，定价和产出决策是根据对竞争者反应的不精确的或不完全的信息制定的。再者，除非我们对企业决策者如何考虑其他厂商决策者所作反应设立特定的假设，否则，要建立模型是困难的。
斯蒂格勒暗中合谋的寡头垄断模型
施蒂格勒模型取消了反应函数。他从垄断寡头愿意勾结起来以使联合利润最大的假设出发。然而，实行合谋成本是很高的，监督实施的费用更高。如果一个行业内所有厂商一起行动，他们可以通过制定产出和价格来使该产业总利润达到最大。垄断利润因而也会存在。但是，寡头垄断出现在一个不完备的世界，因为交易费用并不为零。
在施蒂格勒对寡头垄断的探讨中，垄断寡头的一致目标是合谋；然而，每个人都意识到，没有人会因为存在着合谋协议而让自己的欺骗行为受限制。虽然存在某个用于检查诡计和作弊的最适度的资源量，但是这些资源肯定不足以使垄断寡头勾结得像是一家厂商。总是存在某种偏离任一合谋解的均衡状态，这一合谋解代表通过合谋寡头可达到的最大垄断情形。斯蒂格勒将募头垄断看成为一种公开的或暗中的、在信息完备的基础上形成的卡特尔，其实施措施不完全有效，尽管这种不高的有效性是可以接受的。
开放的寡头垄断
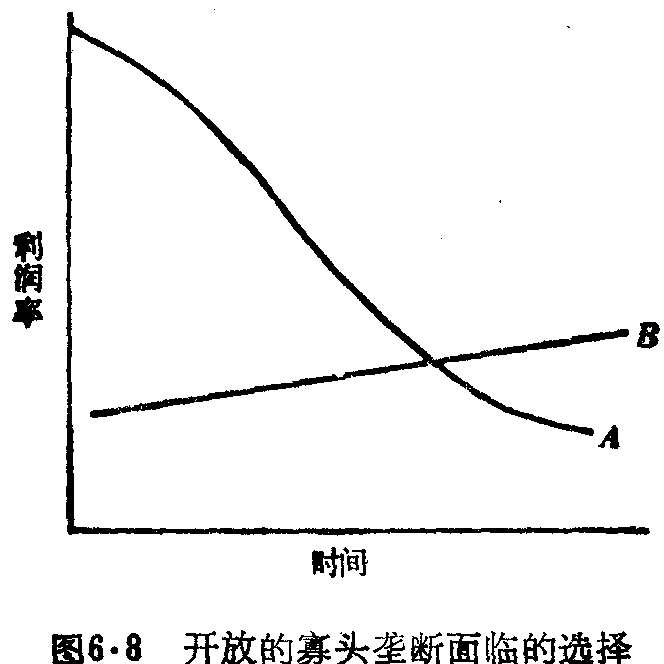
施蒂格勒主要给出的是一个开放寡头垄断模型的基础。该模型预言，寡头厂商可以通过逐渐把市场让给新进入者，来使其利润流量的贴现值最大。因此这种开放模型预言，现有企业将不会制定某个价格以阻止进入，相反，他们将确定较高的价格而使他们的利润流量现值最大。在图6．8中，我们可以见到寡头垄断企业面临的两种选择。如果利润下降序列的最初利润水平足够高的话，它的现值可能超过持续稳定利润率的现值，因此，现有垄断寡头有标明为A和B的两种时间利润率曲线的选择。时间利润曲线A表示由高价格产生的近期的相当高的利润，和随后的以由进入引起的低价而引起的利润下降。时间利润曲线B表示在整个时期略有增长的利润率。依据选用的贴现率，A或B会有最大的现值。如果贴现率比较高，未来获得的利润的现值将较小，时间利润曲线A的现值会比B的现值高。如果贴现率低的话，远期的利润价值较高，时间利润曲线B较受欢迎，因为它将有较高的净现值。
福格（Fog）认为大型寡头垄断企业有一条长时间水平的利润曲线，这意昧着一个低的贴现率。因此他预计，寡头垄断产业在厂商数或其集中率方面是稳定的。这样，基本上说，我们从施蒂格勒的开放寡头垄断模型得到了一个可检验的含意。施蒂格勒模型预示，随着时间的延续，寡头垄断的集中率会下降，而福格模型则预言集中率是稳定的。卡默逊试图检验这两个争执不下的模型。
简言之，卡默逊考察了从1947年到1963年寡头垄断市场的两个无联系的实例，他以75％的四家厂商集中率为截点，发现寡头垄断量在逐渐减少。考察另一组市场，发现考察期内26个行业中有12个行业的四家厂商集中率是减少的，另10个是增加的，还有4个行业保持不变。卡默逊的结论支持了施蒂格勒的开放的寡头垄断模型的假设，尽管他的结论建立在一些限制条件上。毕竟，集中率下降可能是由于在相同时间内的其他影响，诸如反托拉斯的压力或厂商多样化经营的压力所导致。
施蒂格勒模型的其他可检验的含义
施蒂格勒寡头合谋模型的可检验的含义如下：
1．包含的厂商数越少，卡特尔将越有效。较少的厂商数意味着实施卡特尔安排的较低的成本。
2．比较而言，暗中降价常常是针对大顾客而不是针对小买主，因为对任何在给定的降价下，由于大主顾购买量大。从中获益也就大于从小买主那里的获益（假定获知降价的概率相同）。
3．产品越是同质，越容易实施合谋价格协定。当产品为异质时，价格下降可采取改进质量的形式，而且很难避免。
4．产业的需求和成本条件越不稳定，勾结成功的可能性就越小。在必须适应不断变化的需求和供给的条件的产业中，要实施协定就更难。
拗折点需求曲线
经济学家保罗·斯威齐提出的寡头垄断模型暗含无合谋价格刚性的假定。
假设
在斯威齐的模型中，假设市场是那样一些竞争者组成，只要有一家厂商降价，他们就竞相削价攀比；而提价时他们却较为迟缓，不完全跟随。这一假定使我们能设立一条单个垄断寡头面临的需求曲线。
拗折需求曲线的性质
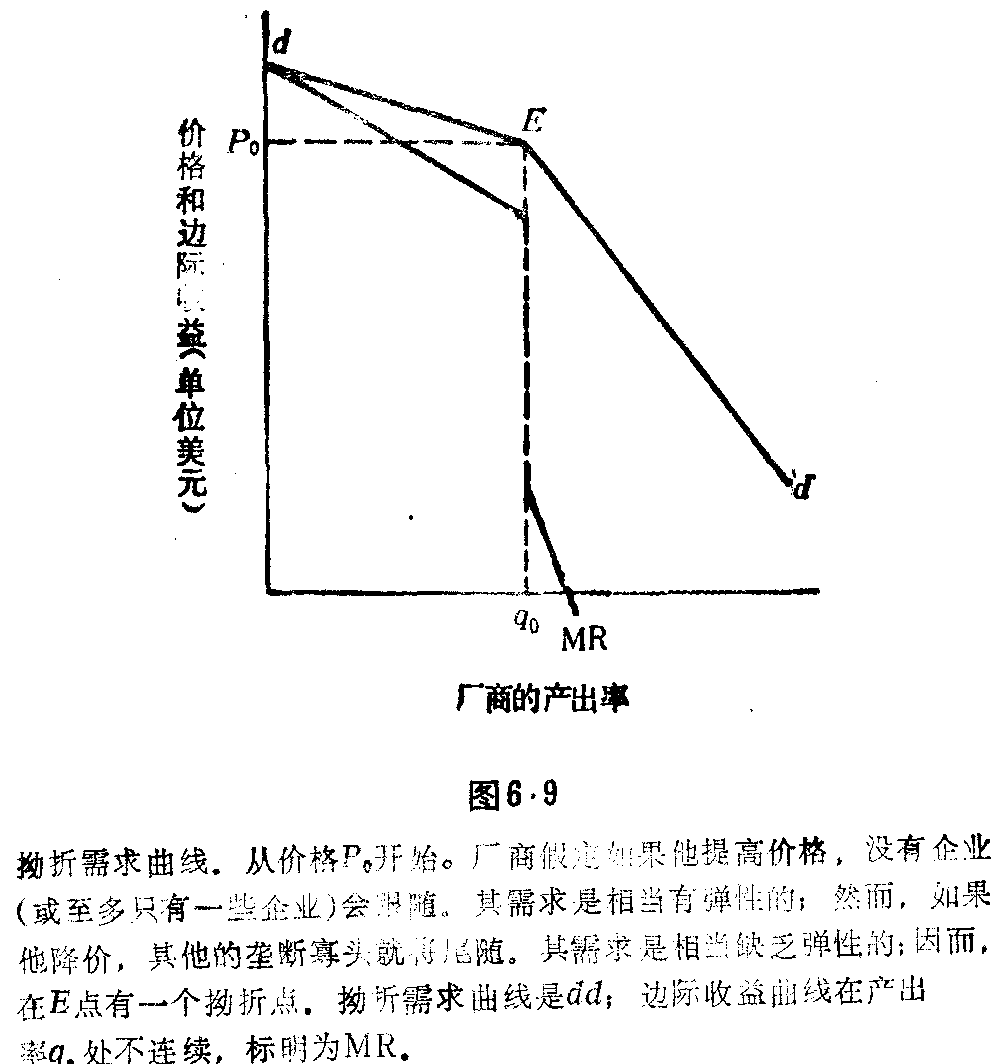
在图6．9中，我们画出了隐含在斯威齐模型中的拗折需求曲线。我们从Po的假定价格出发，假设在这一价格下，这个垄断寡头面对的需求量是q。这个垄断寡头假定，如果他的或她的价格下降，对手的反应是通过降价攀比来避免丧失他们各自的市场份额。因此，垄断寡头降价后的需求最不会急剧增加。在图6．9中，右面的需求的线表示，这部分的需求曲线是相当缺乏弹性的。另一方面，如果垄断寡头提高价格，没有对手会跟随提价。（如果他们真的跟随的话，这种跟随也是不完全的。）因此，这个垄断寡头在较高的价格下的需求量会急剧减少。E点左面的需求线将是比较有弹性的，即E点左面曲线的平坦部分。结果，这个垄断寡头面临的总需求曲线是dd，在E处有一个拗折点。
边际收益曲线
根据图6.9的拗折的需求线，我们首先从纵轴与需求线的弹性部分相应引出一条边际收益曲线（在dd需求线上从上面的d到点E）。然而，在数量qo处，需求曲线突然改变斜率，变得更陡直。在拗折点或在数量qo，边际收益线出现断裂。因此我们发现，不连续部分是由在数量qo处的下垂线表示的。不连续的长度是和在拗折点的需求线上下两部分之间的斜率差异相称的。记住，除了出现缺口外，MR曲线总是把从纵轴到需求线所画的垂直于纵轴的任何水平线分开。
对边际成本波动的反应
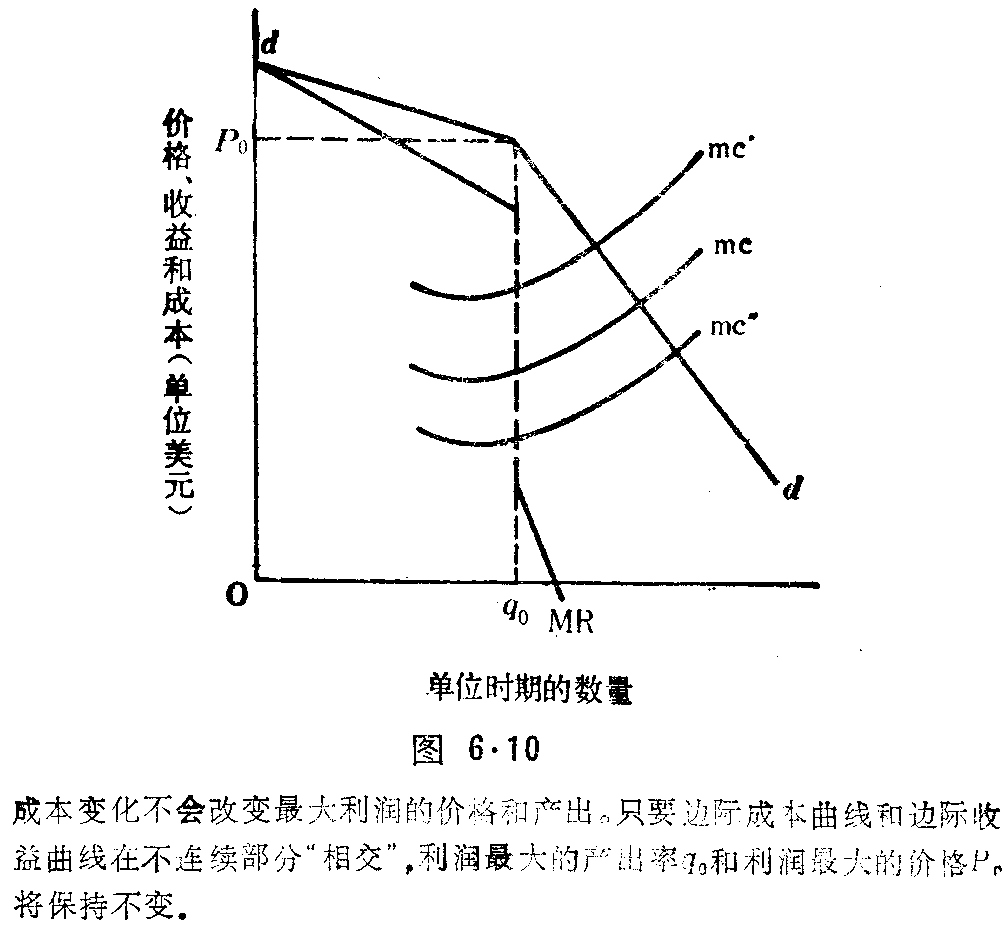
垄断寡头对在边际收益线的不连续部分的边际成本的较小变动无动于衷。例如，在图6．10，假定边际成本是mc。最大利润的产出率是qo，可按价格Po出售。现在，假定边际成本曲线上升到mc’。最大利润的产出率会发生什么变化？没有变化。这个垄断寡头的销售量和产出将保持不变。边际成本下降到mc”，会发生什么变化？没有变化。这个垄断寡头仍按产出率qo生产，按价格Po出售。所以，无论边际成本曲线在边际收益线的不连续部分下降多少，边际成本（在界域内）的波动不会影响价格或产出，利润最大化的条件MR＝MC将保持不变。
对需求变化的反应
需求变化不影响垄断寡头价格的情况也是可能的。然而，这将改变生产量。
考虑一下图6．11中的（a）。这个垄断寡头使利润最大的产出率为qo。最大利润的价格是Po。边际成本曲线和边际收益线的不连续部分相交。
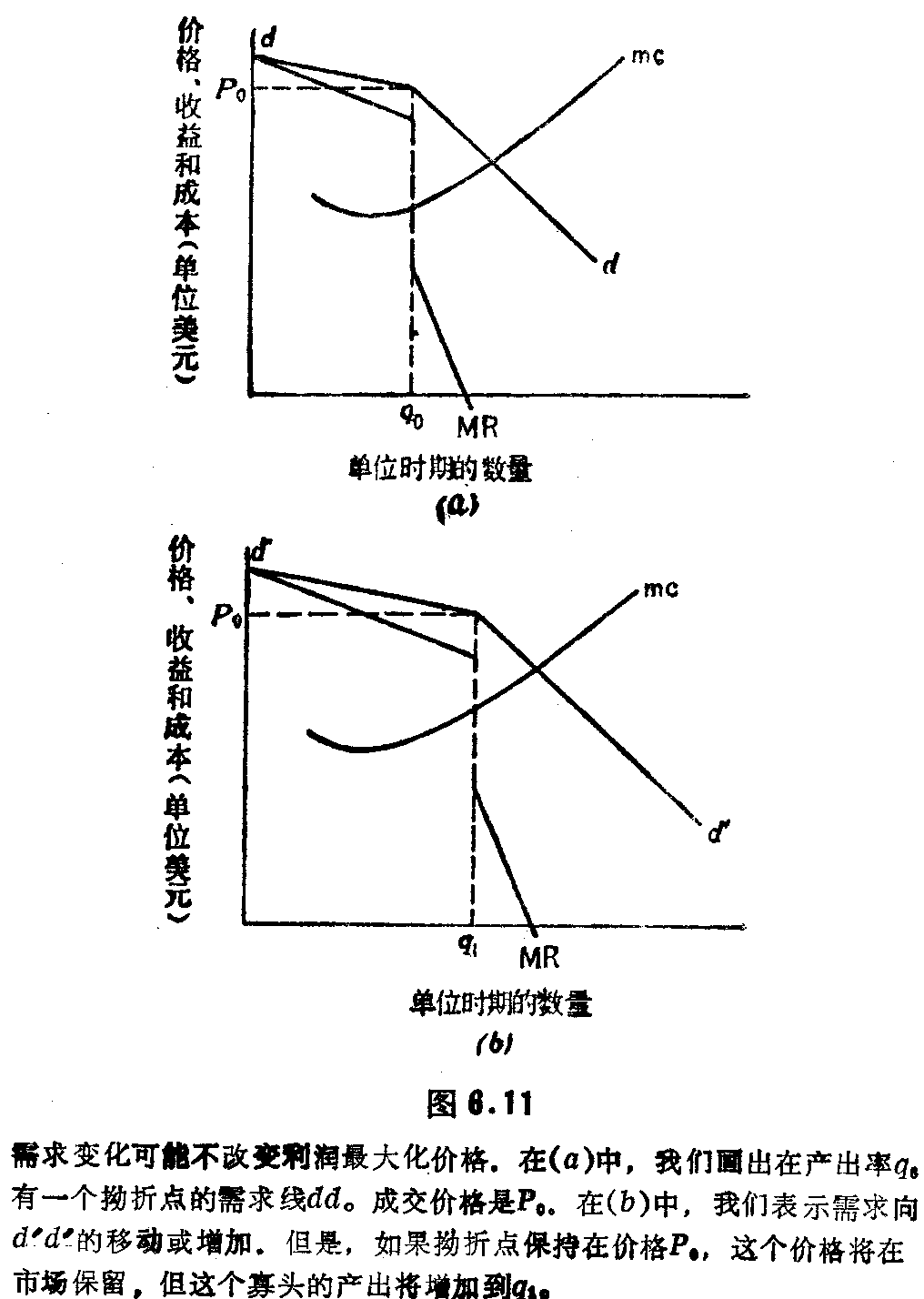
现在，在图6．11中，需求量的变化由（a）的dd到（b）的d’d’。但是，拐折点保持在相同的价格Po。因此，我们假定需求线由dd到d’d’的移动是在曲线的两个不同部分的斜率保持不变的一种严格的外推移动。成本曲线也保持不变。（b）的边际成本曲线mc和（a）的边际成本曲线一样。很清楚，边际成本曲线和新的边际收益曲线在较高的产出率相交，因此最大利润的产出率从qo增加到q1。只要需求增加能使边际成本曲线继续和边际收益线的不连续部分相交，那么即使产出变化，价格也将保持在Po。这个例子也可修改为需求减少。只要需求减少量小到足以允许边际成本线继续和边际收益线在不连续部分相交，结果也是一样的。需求下降的价格将保持不变，但是每个垄断寡头的生产量会下降。
向内拗折的需求曲线
看一下图6．12，我们画出一条在E点有拗折点的需求线。然而，上半部分比下半部分陡。这与我们已经了解的拗折点需求线相反。这种相反的拗折点是以个别垄断寡头预期所有的竞争者都将对他或她最初的提价攀比、但是没人会追随降价为基础的。这种预期大概会发生在通货膨胀期间。
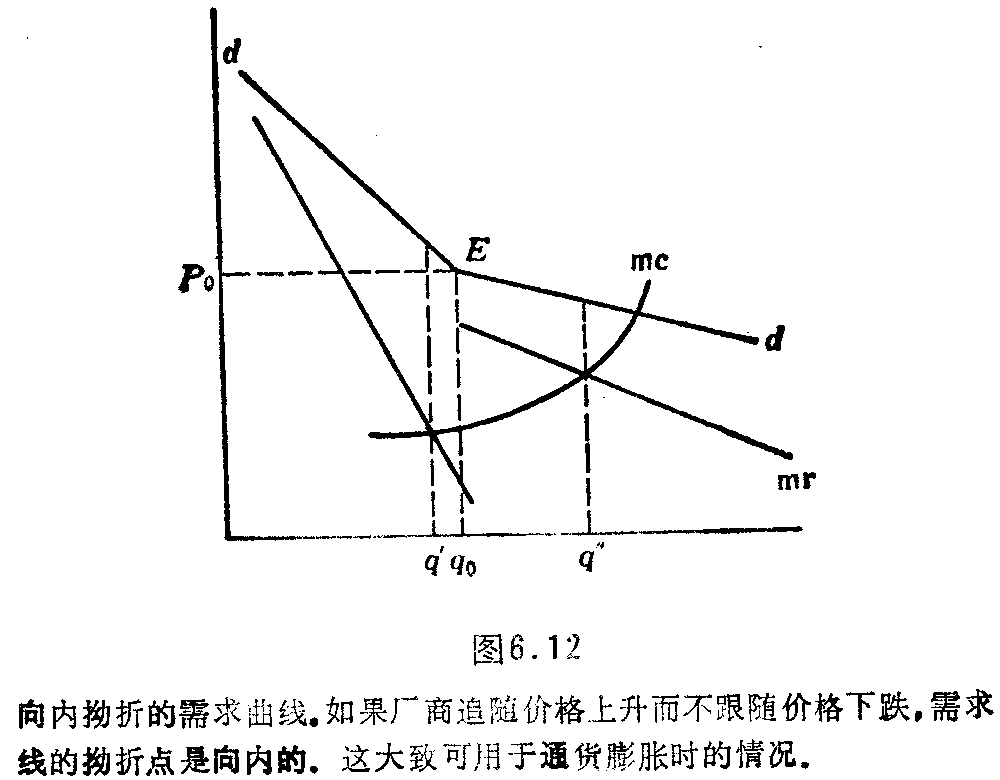
在图6．12中，我们发现向内拗折的需求线产生多个均衡。在产出q’和q”，边际收益都等于边际成本。向内拗折的需求线的这种产出不确定性严重地削弱了这一理论的作用。
对斯威齐模型的批评
斯威齐的论文起初被许多经济学家奉为寡头垄断的绝对新的一般理论。然而，随后的研究和理论分析却对它的通用性提出了怀疑。
理论问题
这一模型有许多理论问题，不少是关于最初价格Po是如何决定的（我们是从假定价格为Po的模型开始的）。如果我们不知道如何达到Po，我们就没有寡头垄断的定价和产出决策的一般理论。
在暂时对竞争者的反应了解不多时，拗折的需求线也许确实是精确的，但很难想象这是一种长期稳定的状况。一些经济学家争辩说，拗折需求曲线适应于一个新产业的早期阶段，或是一个新的、以前不了解的竞争对手进入该市场的产业。
当然，问题是我们的模型仍然是一个非边干边学模型。拗折意念是改变价格来增加利润的一大障碍，而这一障碍完全是寡头人为构想出来的。似乎会有许多方法可以绕过这一障碍。毕竟，这是企业追求的东西——利用一切手段绕过障碍获得较大利润。
经验例证
经验例证并非十分充分地支持拗折点的存在。乔治·施蒂格勒的一项研究表明，在7个寡头垄断产业中，一家厂商的价格上升会引起其他厂商的价格上升。看来不存在竞争对手对拗折需求曲线所固有的价格变化反应的不对称性。这些经验研究并不是否证一种理论，而是对斯威齐关于寡头垄断定价和产出问题的结论的完整性提出疑问。
张伯仑模型
张伯仑也认识到竞争对当事人来说是代价很高的。他指出，假定信息完全并知道每个卖者都能够对市场施加影响，在双寡头的情形了：
［如果］卖者注意到他们对价格的总的影响，价格将是垄断价格……如果卖者是三个或更多个，只要他们每人都关注他的根本利益，那么结果也是一样的。古诺模型中的那种随着厂商数的增加而逐渐接近纯粹竞争价格的趋向是不存在的。
张伯仑的简单双寡头模型
理解张伯仑多厂商寡头垄断模型的最好办法是看一下他的简单双寡头模型。张伯仑假定在第一轮竞争较量后，厂商Ⅰ认识到，厂商Ⅱ对厂商Ⅰ的行动会有所反应。厂商Ⅰ认识到这一点以后，厂商Ⅱ也认识到了这一点。换言之，两个厂商同样认识到他们能做的最好方法是分享垄断利润。图6．13表明了张伯仑的结论。两个厂商使总利润最大的产出率是在边际收益和横轴的交点处，边际成本等于零。这位于产出率Qe。分享垄断的使利润最大的价格将为Pe。因此，每个厂商实际上将生产Qe的一半，并按价格Pe出售。与埃奇沃思的不稳定理论相反，这是一个稳定的双寡头理论。
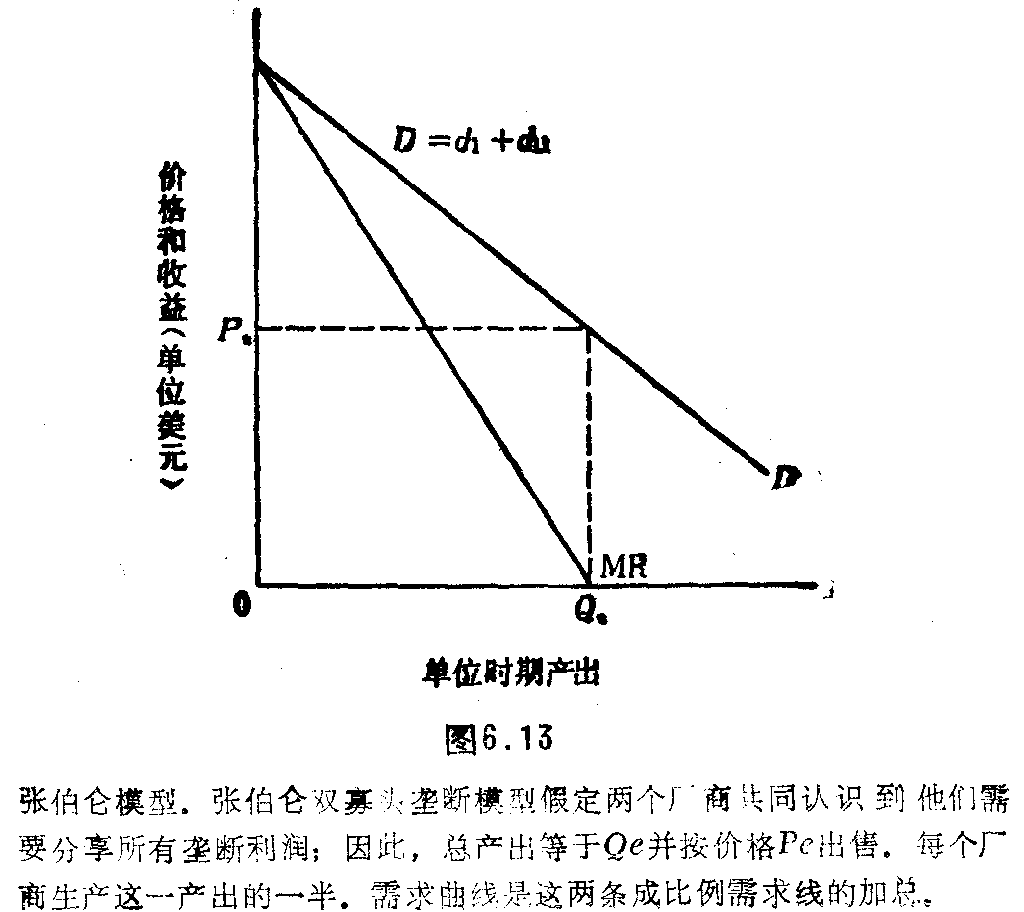
张伯仑模型暗含着一种所有无公开合谋厂商的稳定价格体系。不存在正式的书面或口头的协议，这是一种非合谋行为，它导致的结果和一个完全有效的卡特尔所导致的结果是完全相同的。这样一个模型的问题在于，它隐含着分割共同利润的实施成本为零。如果这一模型可被用来描述两个厂商的情况，那么为什么它不能被用于描述三个、四个或五个厂商的情况？换言之，厂商数量多到哪一点，才使削价动力太大，从而导致暗含的卡特尔破裂？这个模型没有告诉我们答案。
张伯仑模型何时达到竞争价格
张伯仑在表述他的模型何时会解体以达成竞争性的结果方面看来并不非常确定。他说，“在个人对价格的影响变得十分小，以致他忽视了它时，合谋便解体了。”换言之，甚至在有完全的信息和不存在不确定性时，产生竞争结果的唯一条件是：在一个产业里存在着大量的厂商。在张伯仑有大量厂商的世界里，每个厂商都将降价，因为其个别行动几乎没有影响力。这很难与信息完备的假定，瞬时反应的情况，以及厂商力求利润最大化的愿望相一致。张伯仑避开了理论上的这一自相矛盾，他说卖者决不会视自己为造成这种不一致的原因，因为他或她从削价中获得了可得到的各种好处，而这一削价“使其竞争者感受到的不安相对较小。这时，他没有理由去保持有利于他的，对其他厂商无影响的细微价格差异。”
实际上，张伯仑的意思是，少于使单个厂商需求曲线具有完全弹性的任何厂商数都不能保证达到竞争性价格－产量结果。
费尔纳模型
费尔纳（Fellner）给我们提供了一个非合谋的、部分实现总利润最大化的模型。费尔纳基本上是探讨没有明显勾结的垄断寡头的行为。然而，费尔纳讨论的总利润最大化所遇到的障碍对勾结起来的卡特尔和非合谋垄断寡头都是一样的。它们包括：
1．错误和不确定性。
2．个别厂商在利润分割方面玩弄花招，因而阻碍总利润的最大化。
3．各厂商对风险的评价不同。
4．协调非价格变量有困难，如创新率、成本、无法统一的产品差异。
虽然费尔纳承认，参与厂商越多，总利润的最大化就变得越困难，但是他没有分析厂商数量的问题。尽管缺乏分析，费尔纳认为在所有集中的市场中，卖者数量有可能增加，同时竞争和技术进步也会增加。
纳特－莫尔模型
G·瓦伦·纳特（G．Warren
Nutter）和约翰·莫尔（JohnMoore）发展出一种比上述模型更复杂和“更现实”的试验性寡头垄断理论。在纳特－莫尔模型中，每个卖者的价格是公开的。然而，买者和卖者之间存在着信息成本或价格摩擦，为了解每个卖者的价格，他们必须花费时间和其他资源。这是一个贯穿始终的模型；因此，买者和卖者知道未来的盈亏并能将之准确地贴现为现值。买者和卖者共同监督市场价格。如果产业需求线、监督费和贴现率已定，卖者可以形成了解对手将降价多少的规则。然后，主要以卖者在整段时间失去多少销售量为基础，纳特和莫尔设法预测在任一时期内价格将下降多少。尽管我们不详述他们那复杂的模型，但还是可以引用他们的基本结论之一。他们指出，在一个没有摩擦的世界，厂商会对竞争对手发起的任何降价迅速作出反应，随之消除降价的预期盈利。
所以，我们可以得出结论：摩擦对产生竞争是必需的，在价格体系中没有摩擦，就没有竞争行为。
在有摩擦的世界中，一个产业的厂商越多，每家厂商相信自己对该产业未来的价格控制就越弱。因此在厂商众多时，每家厂商都会认为如果自己不降价对手也极有可能降价。
因此，假定其他条件不变，那便如同潜在的定价者所领悟到的那样，降价造成的持久损失会随厂商数的增加而消除。只要价格处于通常限定的竞争性水平之上，有一些厂商——不必“为数很多”——就会使他们中某一家的降价变得有利可图。在正常情况下，价格会确定在竞争性水平，价格等于边际成本。甚至不难想象这样的情况：从长期来看，价格会处于这样的水平，即该产业的少数厂商赚得利润为正。
进一步的结论是，当另一厂商的搜寻强度增加时，卖者的搜寻强度会非常稳定地下降。
看来纳特－摩尔的理论是施蒂格勒的开放寡头垄断理论的扩充。当我们将这两种模型一起考察时，可以发现寡头垄断不完全是垄断的一种形式。而且很明显，随着厂商数的增加，价格的下降量趋向增加。
其他寡头垄断模型－戴注戴姆塞茨
戴（Day）提出的模型假定企业不知道产业需求曲线或对手的反应，即每个卖者都接受给定的价格并按这些价格调整他或她的产量。而且，在投入和产出之间有一个时期的滞后。戴模型得出下述结论：甚至只剩一个低成本的生产者时也会出现竞争均衡。他的竞争结果在任何时候都不依赖市场中的卖者数量。很明显，戴既考虑实际进入，也考虑了潜在进入。
在另一模型中，戴姆塞茨区分了潜在竞争和实际竞争，他争辩说，甚至只有一个有效生产者时也可以有潜在竞争。戴姆塞茨举厂商投标竞争成为电力供应垄断者为例。这些厂商的投标价格竞相降低，直到正好等于包含正常报酬率的平均成本。因此，这一价格将趋向竞争性水平。
博弈理论模型
大约40年以前，冯·诺伊曼和摩根斯坦出版了一本被经济学家誉为寡头垄断市场模型、特别是双寡头垄断理论研究突破性的著作。博奕论可应用于研究许多决策者可能存在的，甚至是真切的动机。例如，假定厂商有两种可供选择的增加利润的策略，在图6．14中，我们列出用以分割10000美元利润的降价和增加广告开支的两种可能采取的策略。纵轴表示厂商A的策略，横轴是厂商B的策略。在博奕中，每个厂商可以降价或增加广告开支来增加利润。数字只表示厂商A选择策略时的利润变化。因为在这个报酬矩阵中，两个厂商的利润总变化被限定为10000美元，厂商B的利润变化为10000美元-A的报酬。假定每个厂商都知道所选择行动的相对报偿，选择时没有彼此依赖。在此例中，如果厂商A选择降价，厂商B的最优战略也是降价，因为B从降价中可获5000美元（10000美元-5000美元＝5000美元），而增加广告费可获4500美元（10000美元－5500美元＝4500美元）。也可以假定A和B都将在降价和增加广告费中选择一个，因为厂商的这种行动将增加总利润。注意，厂商A由降价获得的最小收益是5000美元，增加广告的最小收益是4000美元。结果，A将选择降价，因为这将使该厂商的最小收益最大。这种抉择常被称为“最大化极小值”战略，或使可供选择的各策略的矩阵中横行所示的“最小值”最大。
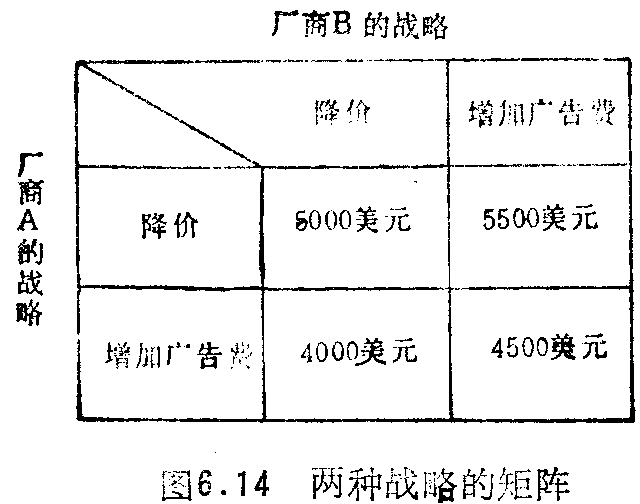
厂商B的战略从每一纵列中所示的使厂商A的报偿最小的各种不同组合中选择。在此例中，B将选择降价，因为这是使相对于A的最小值最大的报偿（或称为“最小化极大值”的极大值）等于5000美元。在这种情况下，两个厂商都选择降价，各得5000美元。这种均衡常被称为“鞍点”，因为厂商A和B在确定对于的行动后都不会改变其最终决定。“鞍点”并非存在于一切报酬矩阵中，这使决策者在做出不同的可行选择时可能采用替代的或混合的策略。
博奕论可以应用于许多厂商，卡特尔化的可能性也会形成一些联合体。马丁·舒别克（Martin Shubik）表明，博弈论已推证出大约40个解，在每个解中，理性行为的可供选择的形式可从解释决策者行为的各种动机中推导出来。
博弈论的一个广为人知的公式是由纳什（Nash）提出的。在纳什均衡中，每一议价者在现状点处都给定出了基数效用。在一个全面而又严格的推导中纳什表明每个决策者的最佳解是使组合产品效用最大的点。
博奕论在识别存在合作动力的复杂状况的某些基本特征时也是有用的。许多情况下的博弈都是古典的囚犯二难推理理论的发展。在这些博弈中，两个犯罪嫌疑犯被分开审问，两人中只能有一人有释放的可能。如果两个囚犯都不承认，那么每个人都将被判在小牢房里监禁6个月。如果一个囚犯承认，而另一个没有承认，则坦白的那个嫌疑犯将免于起诉，而另一个将被判10年徒刑。如果两人都坦白，则每个嫌疑犯将被判5年徒刑。假定两个嫌疑犯都害怕监禁，且他们坦白后也不会增加额外负担，则每个嫌疑犯都将发现坦白是最好的战略。但如果他们串通一气不予承认，则两个人的境况都会变得更好。因此，从嫌疑犯的观点看，达到最好的结果需要信息和联络。这也可以通过建立某种非正式的规则来达到，例如，承认的那个人以后将遭到报复，为此行动承受沉重的代价。拉弗（Lave）发现，在重复囚犯的二难博弈时，被隔离的两个人没有联络也能彼此合作。
对其他企业潜在扩张的忽略
在考察寡头垄断力量时，其他企业的潜在供给常常被人们忽视。下面我们举例说明一个有明显寡头垄断势力的厂商其垄断势力是如何为其他厂商供给弹性的增大所削弱的。我们将举通用汽车公司的例子。
推导一个厂商的需求和所有厂商的供给之间关系
汽车工业多年来一直被视为寡头垄断的例子。在这里，我们想表明的是，尽管通用汽车公司拥有极大的寡头垄断势力，但是这种势力也会受到其他汽车厂商供给弹性的影响。
设通用汽车公司生产qi。则
Qs＝qi＋q0
（6．1）
Qs＝产业供给量
qo＝所有其他厂商的供给
供给和需求是价格的函数，均衡时
QD（P）＝Qs（P）＝qi＋qo
（6．2）
式中，QD＝汽车的市场需求。则
qd＝QD－qo
（6.3）
式中，qd＝对通用汽车公司汽车的需求。换言之，公式左面是对通用汽车公司汽车的需求。
全部说明是
Qs＝产业供给
qi＝通用汽车公司的供给
qo＝所有其他供给
QD＝产业需求
qd＝对通用汽车公司的需求
等式（6.3）中的每一个变量可以有同样小量的变化，以得到
△qd＝△Qd－△qo
（6．4 ）
用qd△P除等式（6.4），得
（6.5）
现在用P乘等式（6.5），得
 （6.6）
整理等式（6.5）。用QD／QD乘右面第一项，用qo/qo乘第二项。
（6.7 ）
但是这等于
（6.8）
这里εo＝其他汽车制造商的供给弹性
η＝需求的价格弹性．
从等式（6.8）中，我们可见通用汽车公司产品nd的需求价格弹性是市场需求价格弹性nD、其他企业供给的价格弹性以及讨论中的这个企业占产业产出相对份额（的倒数）QD/qd。的函数从等式（6.8）中可以知道Eo是重要的。因为n总是负的，当我们去掉Eo时，我们总是绝对增加了这个企业所面临的需求价格弹性。在短期，通用汽车公司产品的需求线也许是缺乏弹性的。然而，在长期，如果Eo足够大的话，情况就不是这样了。这一分析表明了通用汽车公司这样的厂商为什么在一个短期需求缺乏弹性的市场上将价格定得低于预期价格的原因。
一些假设的数字
对新汽车的需求价格弹性的估计是不同的。一个大致的平均数是ηd＝－2。
回想厂商利润极大化时
MR＝P（1＋1/ηd）＝MC
（6.9）
因此，整理等式（6.9），得
（P－MC）/P＝－1/ηd
（6.10）
现在，如果我们假定边际成本大致等于平均成本（对销售几百万辆汽车的企业而言，这不是不合理的假定），则等式（6.10）变为
（P－AC）/P＝－1/ηd
（6.11）
则，如果产业需求价格弹性大致等于－2，我们就可推断
（P－AC）/P＝－（1/－2）＝1/2
（6．12）
这将表明，每一美元中有50美分的边际利润。然而，如果我们看一下通用汽车公司和其他汽车公司的有关资料，我们发现根本没有50％的边际销售利润。我们看到的是更接近6－10％的销售报酬率。在我们使用等式（6.12）时，10％的销售报酬率是和一个有大约－10的需求价格弹性的企业相一致的。
利用这一结果，我们能大致知道通用汽车公司面临的供给价格弹性。我们将ηd＝－10彻ηd＝－2代入等式（6.8）。通用汽车公司所占汽车业产量为50％左右，因此QD／qD＝2，qo／qd＝－1。所以，等式（6.8）变为
－10＝（2）（－2）－（1）εo
（6.13）
其他厂商的供给价格弹性Eo大致等于6。通用汽车公司的汽车每增加1％，将诱发其他公司的供应量增加6％。因此，通用汽车公司的垄断或寡头垄断力量受到汽车业其他厂商供给的限制。
结论
在彼此竞争的寡头垄断模型中，没有一个能够称得上是理论上更正确或经验上更有效的。每种模型都按自己的角度对以厂商为数不多为特征的行业中决策者行为的理解作出了贡献。这些理论主要是提出了判别决策者行为所必需的关键因素，特别是信息的作用和竞争者的行为。尽管许多理论特点类似，如厂商总是力图使总利润最大，但很显然，要协调各厂商定价策略来使总利润达到最大化极其困难的，这需要有企业间的联络、了解交易活动和其他企业的反应。
|